Nicely, no, I’ve lied: not 13, however merely 4 methods of taking a look at (and doing) multiplication are contained herein. And I hope to persuade you that they’re basically the identical mathematically, which could be very a lot my level. There are different methods to calculate the product of two constructive integers, however I need to depart these for an additional dialog.
As we speak’s Commonplace Algorithm
Once I was in main college beginning in 1955, there was just one method introduced for doing multi-digit multiplication (although it had two variants that differed solely cosmetically). I’d wish to discover that method naively (which is to say with out trying on the underlying arithmetic that justifies the process), then take a look at two different fashions/strategies for doing the identical downside earlier than returning to what’s typically considered as we speak because the “commonplace algorithm” for locating the solutions to multi-digit multiplication issues. I’ll conclude with a visible method that some college students discover useful.
Let’s discover the product of 27 x 53. Right here is how I used to be taught to do issues like this:
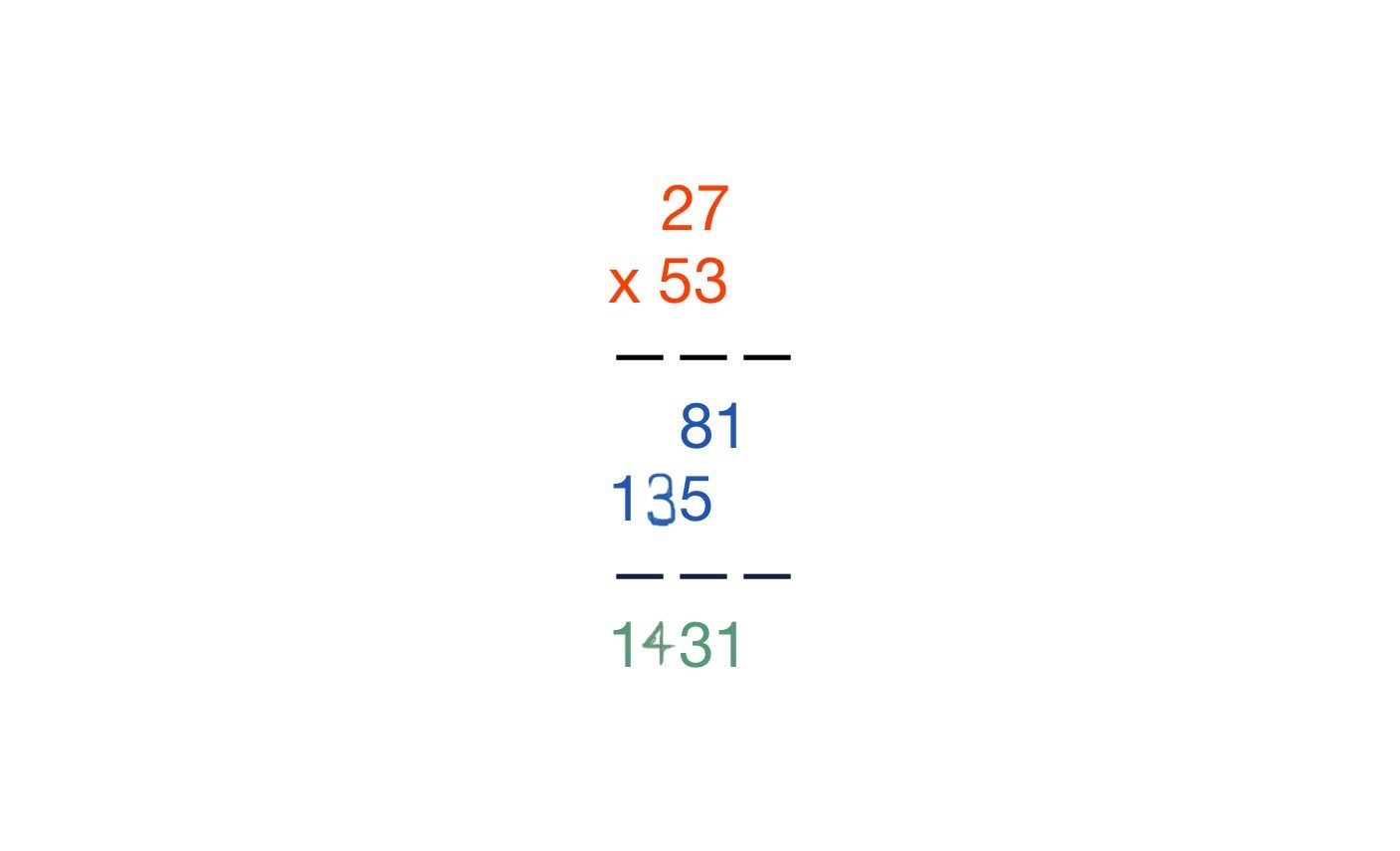
Should you’ve someway forgotten the process (the supply of software program calculators on smartphones, tablets, and computer systems makes handheld-calculators appear virtually quaint, and it’s not inconceivable that utilizing them for arithmetic would lead some folks to develop rusty with paper-and-pencil algorithms), it really works like this: multiply 7 by 3; that’s 21. You write the “1” under the primary line below the three, then both write 2 above the “2” in “27” or mentally maintain onto it (both method, that is referred to as “carrying”). Multiply the “2” in “27 by 3 to get 6, then add that carried “2” to get 8, which you write right down to the instant left of the “1” under the primary line.
At this level, you multiply 7 by 5 and get 35. You write “5” below the 8 and “carry” the “3” above the “2” in 27 or maintain it mentally. Then multiply 2 by 5, yielding 10. Add that carried “3” and write down the ensuing “13” to left of the “5” below the “8.” Now you’re carried out multiplying and should add the 2 traces (often called “partial merchandise” you simply created. Doing so column by column, you get 1431 (I’ll assume you continue to know how you can add two multi-digit numbers).
I can’t communicate for you, however after I realized the above process, I don’t recall the trainer going into a proof of why it labored. We have been simply to imagine that it did, and it was as much as us to do sufficient examples that we “mastered” the algorithm. If we knew our one-digit multiplication and addition details and didn’t get misplaced or marvel about that left-shift enterprise when writing the second partial product, we have been “good.” Many lecturers, mine included, prevented that difficulty completely by telling college students to put in writing a “0” below the right-most digit of the primary partial product after which writing down the digits of the second partial product to the left of that “0” as they have been computed. In some unspecified time in the future, college students have been both instructed in later grades or deduced for themselves that so long as they weren’t careless, it was not strictly essential to put in writing that “0” or a number of “0’s” if the calculation entailed numbers with greater than two digits. Personally, I different between being very cautious and fewer so till the necessity to write in trailing “0’s” merely extinguished itself, however I’ve seen adults who will write each final one among them in. Given my sloppiness and obsession with being “first carried out” in elementary college, I most likely would have benefited from extra warning. I’m positive my lecturers would have appreciated clearer writing of every kind from me. Or maybe we must always have been taught the lattice technique. (See under).
You could have additionally had a trainer who defined what was occurring, however in teaching upper-grade elementary arithmetic lecturers in Michigan in 2004-2006, I noticed many lecturers who weren’t large on why issues they taught made sense mathematically. And for now, I’m going to be a kind of lecturers, although not for too lengthy.
Lattice Multiplication
It seems that the above “commonplace algorithm” has not at all times been commonplace in any respect. In reality, earlier than the widespread use in Europe of the printing press with moveable sort after its invention by Johannes Gutenberg round 1440, the most typical strategy to do multi-digit multiplication was the lattice (aka, “gelosia” – associated to the English phrase “jalousy”) technique, first launched to Europe round 1200 by Leonardo of Pisa, higher often called Fibonacci). Let’s see how the lattice technique works on our beforehand solved instance, 27 x 53:
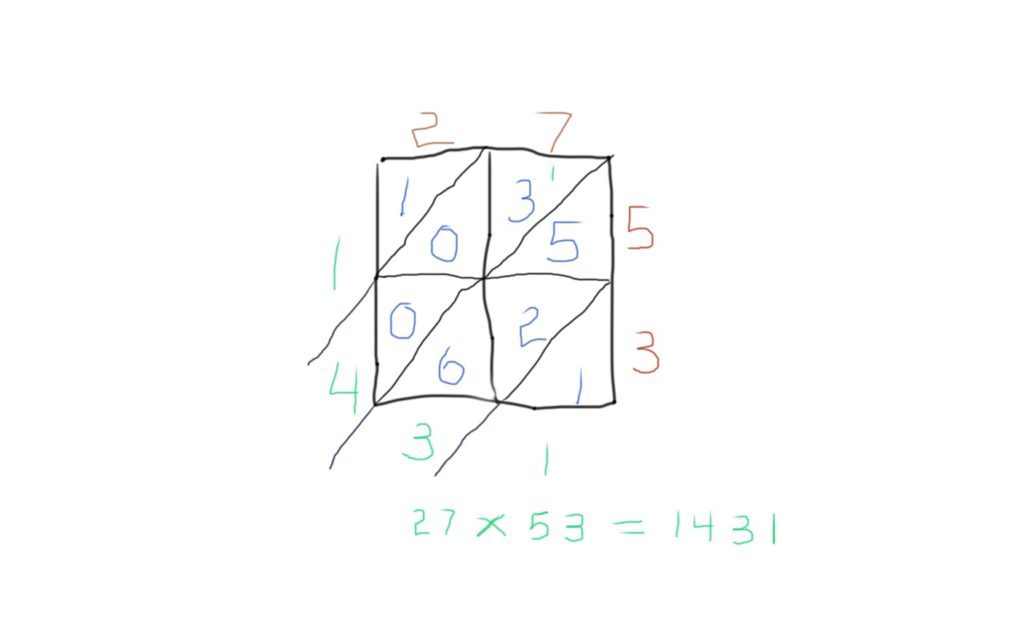
What’s occurring right here? The 2 elements, 27 and 53, are written – one digit per column or row – above or to the precise of the lattice, respectively. Beginning within the higher right-hand nook, 7 is multiplied by 5 to acquire the two-digit product, 35. These digits are then put into the higher and decrease halves of the corresponding cell. The method is repeated in every cell: 7 x 3 for the decrease proper cell, 2 x 5 for the higher left cell; 2 x 3 for the decrease left cell. Notice that on this final case, the place the product is simply a single digit, 0 is put within the higher half of the cell as a place-holder.
At this juncture, the multiplication course of is full, and the outer digits of the elements don’t determine additional within the calculation. As an alternative, we add diagonally, beginning within the decrease proper of the lattice, the place we merely have “1.” The following diagonal yields the sum “5 + 2 + 6,” and the primary digit of the ensuing “13” goes on the backside, whereas the “1” is carried into the subsequent diagonal the place it’s added to “3” to present the sum, “4.” Lastly, the “1” within the higher left diagonal is introduced down and we learn from there down after which proper to get the whole product, 1431.
Once I first noticed this method demonstrated by a fifth-grade trainer I used to be teaching in Pontiac, MI, he supplied no rationalization of the method, only a assertion of every step. I assumed this was as a result of within the EVERYDAY MATH curriculum the scholars have been utilizing, they’d been taught lattice multiplication in fourth grade and have been now revisiting it for merchandise involving decimals. I checked the consequence with the usual algorithm and satisfied myself that it was appropriate, however didn’t get why it labored mathematically. I did one other instance to make certain I might do the process precisely, then approached this trainer after class to ask him concerning the underlying mathematical justification for the strategy. Apparently considering that I didn’t observe the steps, he began to do one other instance, however I assured him that my query was not concerning the process however about why it labored. He checked out me as if that have been a wierd factor to wish to know.
That night time, I sat down and shortly noticed that my confusion was merely with the diagonal addition. The association of the lattice was designed to maintain every digit of a partial product aligned with others that had the identical place worth. In the course of the addition course of, single digits with the proper place worth have been added and any sums better than 9 have been “carried” into the subsequent diagonal. In different phrases, this “new” technique was in each respect the identical as the usual algorithm, however with diagonals changing columns and the splitting of cells preserving digits completely aligned correctly, not like typically was the case with college students or adults who wrote the partial merchandise carelessly after which launched addition errors because of misalignment. So the diagonals beginning within the decrease proper represented those, tens, a whole bunch and hundreds digits of the partial merchandise, and naturally the ultimate addition gave the identical consequence as did the usual algorithm. This isn’t a coincidence.
Let’s flip to a different method to take a look at our downside, in a type of “expanded notation.“[ii] I’ll rewrite 27 x 53 as (20 + 7) (50 + 3), noting that this can be a completely legitimate strategy to regroup a number of multi-digit numbers for any objective, although it’s actually not the one method to take action). Now, benefiting from the distributive property of multiplication over addition for the integers, I can multiply these elements as follows: 20*50 + 20*3 + 7*50 + 7*3. This equals 1000 + 60 + 350 + 21, which then yields the sum, 1431. That’s comforting since we’ve got already established two different ways in which the product we search is 1431.
Now we will look extra productively at each the usual algorithm and the lattice technique. Recall that the usual method seems like this:

Revisiting the Commonplace Algorithm
Inspecting the method by which we arrived at this consequence a bit extra fastidiously, we’d word that there’s a whole lot of “mendacity” occurring in our heads after we do the algorithm. After step one (“multiply 7 x 3”) practically every thing we are saying to ourselves is a lie. For instance, the subsequent step is “2 instances 3.” However is it actually? That “2” is within the tens place, and therefore it will be extra correct to say, “twenty instances three is sixty, and we had twenty a couple of in our first multiplication of seven x 3, so including that twenty to sixty provides us eighty, not eight.” In fact, it will be cumbersome to undergo that a lot chatter to do elementary arithmetic, so we don’t. However we don’t for an additional motive: we’re by no means instructed to consider what we’re really doing. All the pieces is decreased, time and time once more, to single-digit multiplication. Place worth is successfully pushed below the rug all through the method.
We subsequent say to ourselves, “seven instances 5 is thirty-five.” However we don’t write that 5 below the one within the first partial product. Why not? Place worth. With out actually being instructed why, we transfer the second partial product one place left, which successfully multiplies that whole line by 10. Had been there extra digits leading to extra partial product traces, every could be shifted left to account for adjustments in place worth. So just like the second multiplication within the first partial product, we’ve got a items digit (“7”) multiplied by a tens digit (“5” which stands for “50”) and our precise consequence there’s 350, not 35.
The ultimate multiplication isn’t 2 x 5 however 20 x 50, which is 1000, not 10. Happily, our senseless left-shifting takes care of that and the 1 representing one-thousand winds up conveniently within the hundreds column for the addition steps.
“Expanded” Notation
Breaking down every multiplication with out this framework, however making an allowance for the precise place worth, we get simply what we bought with the so-called expanded notation course of: 1000 + 350 + 60 + 21 = 1431 (or if you happen to favor, within the order of precise calculation, 21 + 60 + 350 + 1000 = 1431).
Why don’t we see any of these numbers after we use the usual algorithm?
As a result of we mix pairs of steps by addition, leaving us with solely two numbers so as to add on the finish as a substitute of 4. In our want for “effectivity,” we lose transparency in the usual “lengthy multiplication” algorithm. Certainly, as I’ll discover in a future piece, one thing comparable occurs in the usual lengthy division algorithm, the place a good better opacity for many individuals outcomes. With multiplication, what will get hidden is probably not fatally complicated for a majority of younger college students, however for many who “don’t get it,” the wrestle to memorize a sequence of poorly understood steps, maybe exacerbated by a less-than-firm mastery of single-digit multiplication and/or addition details, can simply result in confusion, frustration, and inaccuracy. Shedding readability of reasoning for a achieve in pace isn’t an issue if you’re good at a given process and/or don’t care whether or not you perceive why it really works (as apparently was the case for that fifth-grade trainer and the lattice technique). For a dad or mum, trainer, or learner to see arithmetic as strictly a matter of barely grasped, tenuously memorized guidelines and procedures, there’s a nice threat of making a nation by which an enormous variety of residents “can’t do math,” which is to say that they discover what they consider math to be – calculation – a tedious, intimidating, irritating, and in the end pointless enterprise.
Trying once more on the lattice technique, you may discover that studying the internal diagonals from high left to backside proper, you possibly can see them as representing 1000 + 21, 60, & 350 (appending the mandatory zeros). Or taking every cell individually and by way of place worth, we’ve got 1000, 350, 60, and 21. Those that doubt that the lattice technique “is smart” ought to actually take into account that it’s no LESS clear than the usual one, and presumably a bit extra clear. As for another objections (takes too lengthy to create the lattice, makes use of an excessive amount of room/paper), I’ll depart these for attainable feedback and for a deliberate interview with mathematician James Tanton within the context of fixing quadratic equations and utilizing lattices.
Lengthy Multiplication Visually: An Space Mannequin
Let me supply one final mannequin/technique for doing lengthy multiplication. Earlier than doing so, I must clarify to readers that that is meant strictly to advertise understanding and to enchantment to learners and lecturers who get pleasure from a visible taste to their mathematical comprehension. It’s commonly known as the realm mannequin. Unsurprisingly, I’m going to once more make use of 27 x 53 as an instance the mannequin, proven under:
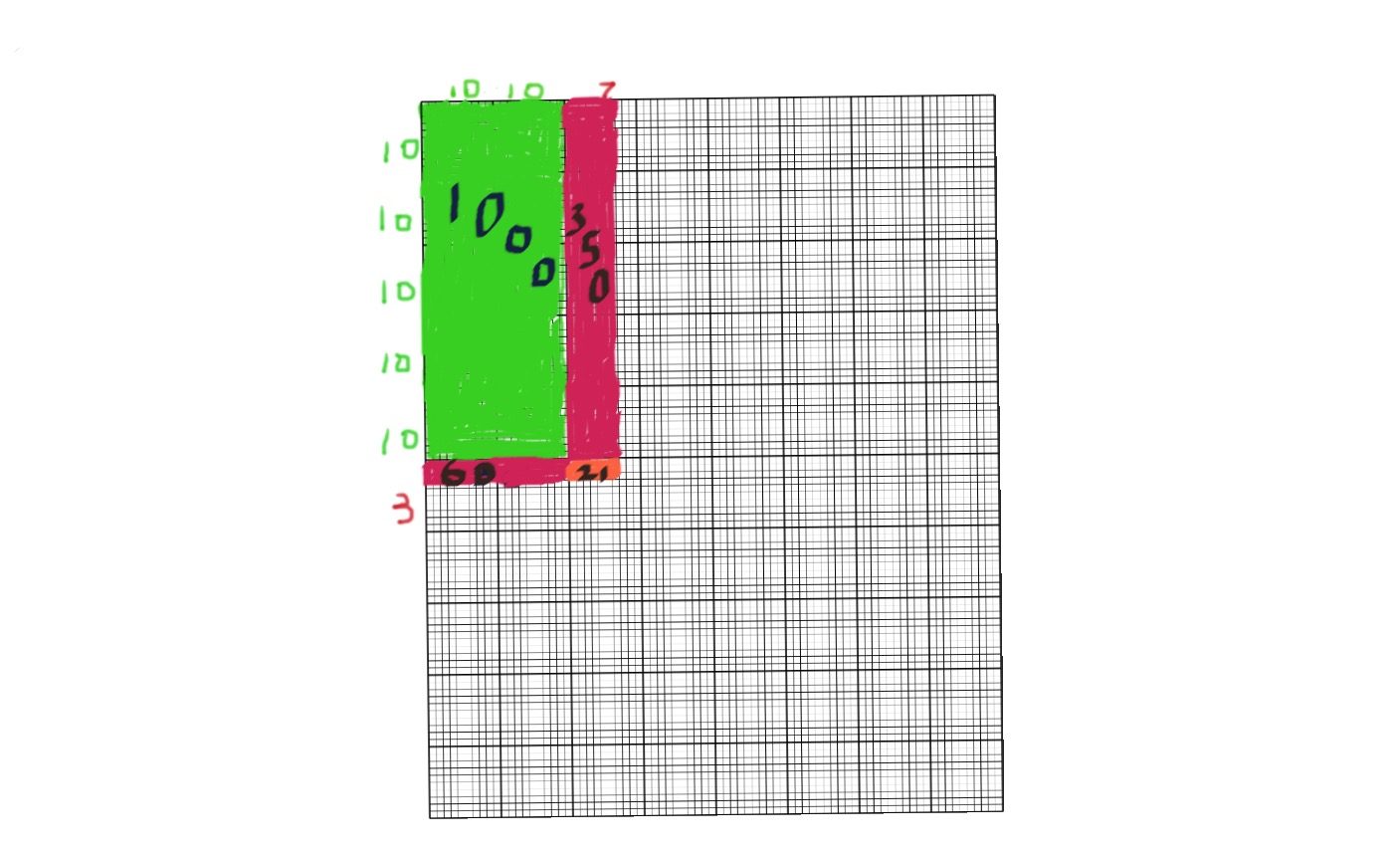
On this mannequin, every massive sq. is 10 x 10 and thus has 100 small unit squares. Throughout the highest, college students will mark a line alongside the horizontal one full block for each 10, and one smaller line alongside the highest of every unit sq., then equally down the left border for the second issue. Right here, I’ve marked two “10’s” and 7 “1’s” alongside the highest, and 5 10’s and three 1’s down the left facet to point 27 and 53, respectively. I used inexperienced to paint in every full hundred-square, pink to paint in every ten “stick,” and orange for every unit sq.. Since we’ve got two by 5 10’s, the inexperienced space covers 1000 unit squares; vertically we’ve got seven by 5 sticks for 350; horizontally, there are three by two sticks for 60. Lastly, there are 3 by 7 unit squares for 21. Including up the areas provides 1431, after all.
In my expertise with elementary college students, having them mannequin a few multi-digit multiplication issues this manner is satisfying for many and significantly clarifying for some who don’t achieve a strong understanding from extra symbolic fashions alone, no matter notation or algorithm. However it’s clear to most college students with out being instructed that doing an space mannequin drawing goes to be far too tedious and time-consuming for an every-day technique of computing merchandise. I’ve by no means needed to inform a scholar that this isn’t meant as a go-to method, although I do attempt to make that crystal-clear to lecturers and fogeys, significantly those that are suspicious of something however the usual algorithm. Quantity-lines, algebra tiles, and numerous different hands-on, software program, and different fashions and instruments are helpful for selling understanding: few are meant to be replacements for or options to the usual algorithms. There are some different algorithms, as we’ve seen, comparable to lattice multiplication, that arguably are a matter of non-public choice, significantly for college students who wrestle to do paper-and-pencil arithmetic the usual method. As a trainer, I don’t see it as my job to dictate which mathematically wise calculation technique a person settles upon, so long as s/he’s making a fairly knowledgeable selection. Refusal to even take into account a couple of strategy to do one thing mathematically is usually the signal of somebody who shouldn’t be assured about arithmetic.
I hope that readers take away from this piece the belief that any mathematical process has to make sense, that those that work can at all times be justified, and that many strategies are intimately associated if you happen to look extra deeply. Within the close to future, I hope to unpack lengthy division in methods that may assist it make extra sense and fewer of a process to be imitated with out understanding.
[i] For these unfamiliar with Twentieth-century American poetry: https://bit.ly/2nWvCYv
[ii] This isn’t the same old definition of expanded notation in arithmetic, however it’s shut sufficient for my objective right here.

Michael Paul Goldenberg




![Erratum for “An inverse theorem for the Gowers U^s+1[N]-norm”](https://azmath.info/wp-content/uploads/2024/07/2211-erratum-for-an-inverse-theorem-for-the-gowers-us1n-norm-150x150.jpg)

