Hobbes: “A brand new decade is arising.”
Calvin: “Yeah, huge deal! Hmph. The place are the flying automobiles? The place are the moon colonies? The place are the private robots and the zero-gravity boots, huh? You name this a brand new decade?! You name this the longer term?? HA! The place are the rocket packs? The place are the disintegration rays? The place are the floating cities?”
Calvin and Hobbes
by Invoice Watterson
December 30, 1989
Certainly, the place are the flying automobiles, the clever robots, the bases on the Moon, the atomic powered lawnmowers? Forty years in the past futurists confidently predicted all of these items in our time. A few of these predictions have been undoubtedly unjustified hype. Nonetheless, the predictions have been extra cheap than might now appear the case. Energy and propulsion applied sciences skilled dramatic progress for nearly two centuries from the introduction of the separate condenser steam engine within the 1770’s till the manned touchdown on the Moon in 1969. This progress included each regular evolutionary progress and a number of other technological revolutions: the separate condenser steam engines, the excessive stress expansive steam engines, inner combustion engines, the electrical battery, electrical mills and motors, the diesel engine, jet engines, rocket engines, and atomic energy. Progress in energy and propulsion expertise has been very restricted during the last forty years.
So too, progress in lots of different areas starting from synthetic intelligence to elementary physics has been fairly restricted. This has made electronics and computer systems extremely seen with society pinning its hopes for a greater future on these fields, in a approach that was not the case with comparable advances previously — radio and tv for instance — that have been overshadowed by dramatic advances in energy, propulsion, and different applied sciences. In all probability numerous elements, together with simply plain dangerous luck in some circumstances, have contributed to the restricted scientific and technical progress of the final forty years. This text will give attention to extreme reliance on symbolic manipulation instead of the conceptual reasoning and conceptual leaps normally concerned in main scientific or technological breakthroughs.
What’s symbolic manipulation?
The traditional Greeks knew arithmetic as arithmetic and geometry. Arithmetic consisted of addition, subtraction, multiplication, and division of numbers. The Greeks had a crude quantity system much like the Roman Quantity system acquainted to most college students at this time (I = 1, V = 5, X = 10, L = 50, C = 100, and so on.). Geometry consisted of phrases and footage, verbal proofs, derivation, or calculations, and diagrams constructed with a compass and ruler. When it’s stated the Greeks may discover the roots of sure quadratic equations, this meant performing visible geometric operations with a compass and ruler. When the Greeks referred to the sq. of a quantity, they meant a literal sq. drawn on a chunk of paper. This type of arithmetic is discovered within the works of Euclid, Archimedes, and Apollonius of Perga. It grew to become the usual in Europe for over fifteen hundred years. Johannes Kepler wrote his ebook New Astronomy, printed in 1609, detailing the invention of the elliptical orbit of Mars and the exact mathematical regulation of planetary movement alongside the ellipse on this type. Isaac Newton used an identical type in his well-known Principia printed in 1687.
In about 1600, the French mathematician Francois Viete launched the idea of utilizing letters to symbolize arbitrary numbers, what we now name variables. Viete’s system was crude by trendy requirements. He used solely vowels to symbolize variables and consonants for constants. It took a number of generations for symbolic arithmetic to mature and exchange the standard Greek type of phrases and footage. Arithmetic and physics have moved within the route of accelerating reliance on symbolic arithmetic and abstraction since then.
Most individuals encounter symbolic arithmetic in highschool algebra. For instance, what’s [tex] x [/tex] in:
[tex] x $+$ 3 = 5 [/tex]
This may be solved simply by subtracting the quantity three (3) from either side of the equation.
[tex] x = 5 $-$ 3 = 2 [/tex]
With symbols, this answer could be generalized to a whole class of issues:
[tex]x $+$ a = b [/tex]
Then, subtract [tex] a [/tex] from either side of the equation.
[tex]x = b $-$ a [/tex]
This can be a normal answer for all equations of the shape [tex] x + a = b [/tex]. Up to some extent, this normal answer might be true impartial of the interpretation or which means of the symbols [tex]x[/tex], [tex]a[/tex], and [tex]b[/tex]. That is a part of the ability and enchantment of symbolic arithmetic. It’s also one of many pitfalls of symbolic arithmetic. In physics or engineering, what if the phenomema represented by [tex]x[/tex], [tex]a[/tex], and [tex]b[/tex] don’t even have the properties of numbers? On this pc age, one other necessary side of symbolic formulation, equations, and options is that they are often programmed on a pc. Basically all pc programming languages have been designed to include variables and at the least easy symbolic arithmetic involving addition, subtraction, multiplication, and division. Some programming languages and environments resembling Matlab and Mathematica can deal with fairly superior symbolic arithmetic. Some programming languages and environments resembling Mathematica and Maxima (previously referred to as MACSYMA) can carry out sure kinds of symbolic manipulations, automated theorem proving, and different unique capabilities.
The instance above may be very easy. Symbolic arithmetic could be rather more advanced and remedy rather more troublesome issues. A tougher downside that took many centuries to discover a answer is the overall answer for the quadratic equation. That is normally taught in highschool algebra. It’s really uncommon in on a regular basis life, however sometimes surfaces as an actual downside in pc graphics. That is an instance of a quadratic equation:
[tex] x^2 $-$ 2x + 1 = 0 [/tex]
This equation has a easy answer. It may be factored into two phrases:
[tex] (x $-$ 1)(x $-$ 1) = 0 [/tex]
The answer is [tex] x = 1 [/tex]. Generally, the sq. of [tex] x + a [/tex] is:
[tex] (x + a)(x + a) = x^2 + 2a + a^2 [/tex]
With some thought, this really provides us a technique to remedy the overall quadratic equation:
[tex] ax^2 + bx + c = 0 [/tex]
the place [tex]a[/tex], [tex]b[/tex], and [tex]c[/tex] could be any three numbers. In a nutshell, we need to reorganize the equation so it’s within the type:
[tex] (x+e)^2 = f [/tex]
This is called “finishing the sq.”. First, divide either side of the overall quadratic equation by [tex]a[/tex]:
[tex] x^2 + frac{b}{a}x + frac{c}{a} = 0 [/tex]
To show the left hand facet into [tex](x+e)^2[/tex], [tex]frac{b}{a}[/tex] have to be [tex]2e[/tex]. So, subtract [tex]frac{c}{a}[/tex] from either side of the equation:
[tex] x^2 + frac{b}{a}x = -frac{c}{a} [/tex]
Then, add [tex] (frac{b}{2a})^2 [/tex] to either side of the equation.
[tex] x^2 + frac{b}{a}x + (frac{b}{2a})^2 = -frac{c}{a} + (frac{b}{2a})^2 [/tex]
Now, the equation is within the type [tex] (x+e)^2 = f [/tex] the place [tex] e = frac{b}{2a} [/tex] and [tex] f = -frac{c}{a} + (frac{b}{2a})^2 [/tex]. Subsequently:
[tex] x + frac{b}{2a} = sqrt{ -frac{c}{a} + (frac{b}{2a})^2 } [/tex]
Then, subtract [tex] frac{b}{2a} [/tex] from either side of the equation and take away the issue [tex] frac{1}{2a} [/tex] outdoors the sq. root signal to get the system for [tex] x [/tex].
[tex]x = frac{-bpmsqrt{b^2-4ac}}{2a}hspace{2cm}aneq0[/tex]
That is the overall answer for the quadratic equation in symbolic type. As soon as once more, up to some extent, this system is appropriate no matter whether or not [tex]a[/tex], [tex]b[/tex], [tex]c[/tex], and [tex]x[/tex] discuss with distances on a surveyor’s map, distances in a blueprint of a constructing, a machine, or an electromagnetic discipline. The reply appears to be present in a exact, step-by-step logical process seemingly devoid of unpredictable and generally flawed instinct.
Most highschool algebra textbooks cease at this level and point out the existence of normal options to the cubic and quartic equations:
[tex] ax^3 + bx^2 + cx + d = 0 [/tex] (Cubic Equation)
and
[tex] ax^4 + bx^3 + cx^2 + dx + e = 0 [/tex] (Quartic Equation)
This apply in highschool algebra textbooks is considerably deceptive and possibly contributes to magical fascinated by the ability of symbolic manipulation. The answer to the quadratic equation by symbolic manipulation entails solely a couple of dozen steps that are usually spelled out step-by-step (as above) in a highschool algebra textbook. As mathematical issues turn out to be extra advanced, the doable symbolic manipulations develop, typically exponentially, in quantity. A profitable answer to an issue in greater arithmetic might contain tons of, 1000’s, or much more steps. There are a lot of doable rearrangements of the symbolic formulation that lead nowhere, a lot as there are various selections in a sport of chess that lead solely to defeat. The variety of doable sequences of substitutions and different symbolic manipulations grows past the restricted potential of human beings to exhaustively attempt every sequence and sometimes past the capability of a pc program, as highly effective as computer systems have turn out to be, to exhaustively attempt every doable sequence. Thus, the mysterious human “instinct” reappears. Mathematicians develop a way of the sequence of steps that’s more likely to end in a helpful reply. Even so, they’re typically flawed and must make repeated makes an attempt — trial and error — to discover a helpful outcome, however many much less trials than an exhaustive brute power search.
The Standing of Symbolic Manipulation
Symbolic arithmetic and symbolic manipulation have acquired nice standing and a repute bordering on magic each basically society and far of the scientific, engineering, and mathematical group. Not with out good motive. Symbolic manipulation has solved many issues and undoubtedly will proceed to take action. Nonetheless, it has substantial limitations relative to human talents and judgement, our conceptual reasoning talents as might be mentioned additional under.
In all probability the epitome of the mystique of symbolic arithmetic and manipulation basically tradition is the well-known equation:
[tex] e = m c^2 [/tex]
This cryptic equation grew to become intently related to Albert Einstein and the atomic bomb. Within the equation, [tex]e[/tex] represents power, [tex]m[/tex] represents mass, and [tex]c[/tex] represents the velocity of sunshine. Within the Particular Principle of Relativity one can derive this equation to point out an equivalence between mass and power. The atomic bomb derives its monumental harmful energy from the conversion of a fraction of a p.c of its mass into power. A bomb that transformed all of its mass into power could be tons of of instances extra highly effective than probably the most highly effective thermonuclear weapons within the arsenals of the main nuclear powers.
The final press, standard science, textbooks and lots of different sources steadily show footage of scientists, engineers, and mathematicians standing in entrance of blackboards coated with cryptic symbols, reinforcing the message that the symbolic arithmetic and manipulations is the essence of science, engineering, and arithmetic.

Richard Tolman and Albert Einstein |
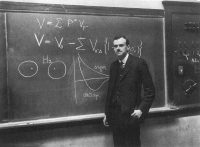
Paul Dirac |

Theodor Von Karman |

Ed Witten |
The nineteenth and twentieth century noticed the regular “professionalization” of science and engineering. This accelerated throughout and after World Battle II which noticed an enormous enlargement within the measurement, the scope, and the extent of public funding of scientific analysis and technological invention, a lot of it related to army analysis and improvement. Tons of of years in the past, science and engineering, invention and discovery, have been performed by a hodge podge of typically rich amateurs, craftsmen resembling clockmakers, blacksmiths, bicycle makers (the Wright Brothers), and college professors who typically relied on educating moderately than analysis grants for his or her revenue. Prizes for innovations and discoveries, in precept (if not at all times in apply) open to anybody, moderately than proposal-driven grants and R&D contracts to particular researchers or analysis teams have been rather more frequent. This modified steadily over the nineteenth and early twentieth century. Germany, particularly, witnessed the rise of an expert civil-service of college professors conducting primary and utilized scientific analysis. Most of the German customs have been intentionally copied in the USA or imported with the large wave of refugees from Nazi Germany.
The professionalization of science and engineering was accompanied by an rising emphasis on the significance of arithmetic and symbolic arithmetic. Within the ideally suited, the skilled scientist or engineer would conduct sober logical scientific analysis, carry out refined calculations or derivations appropriately the primary time via rigorous skilled coaching, and produce scientific and technical advances as wanted, avoiding the messy instinct and time consuming, unpredictable trial and error of the mere “inventor” or “tinkerer.” The fact, after all, by no means matched this ideally suited, however the monumental success of wartime initiatives such because the Manhattan Challenge, the German V-2 rocket program, and lesser recognized successes such because the Jet Assisted Take Off (JATO) rockets in the USA (all these initiatives led by German or German-trained scientists and engineers — J. Robert Oppenheimer with a Ph.D. from the College of Gottingen, Werner Von Braun, and Theodor Von Karman) contributed to the credibility of this image of the central position of symbolic arithmetic, and symbolic manipulation particularly, within the post-World Battle II skilled science and engineering. In response to the semi-official historical past of the Manhattan Challenge, the atomic bomb succeeded on the primary check, a exceptional achievement within the historical past of invention the place repeated failures and repeated trials have been the norm, based mostly partially on purely theoretical calculations by Hans Bethe, J. Robert Oppenheimer, and different theoretical physicists, giving nice credibility to mathematically pushed science and engineering.
The primacy of symbolic manipulation supplied a comforting world by which the scientist, engineer, or mathematician could be an mental plumber, assigned to resolve a particular slender downside in a particular time with out trial and error and with out having to take care of any “huge image” points, “above his pay grade” in government-speak. Coverage makers, enterprise leaders, and the generals who dominated the huge army R&D equipment of the submit World Battle II world may take care of the necessary points whereas assigning the answer of a particular downside to a slender technical professional. Conceptual evaluation is more likely than symbolic manipulation to boost uncomfortable and generally explosive points. In his well-known ebook New Astronomy, Johannes Kepler, a religious Lutheran, devoted a lot of the introduction to arguing that his discovery of the elliptical orbit of Mars didn’t in truth battle with the Bible, which appears to state that the Earth is stationary and the Solar strikes across the Earth in a couple of locations (such because the Ebook of Joshua when God miraculously stops the Solar in its path). Certainly, the wiser contemporaries of Galileo and Kepler suggested each males to current their discoveries as mere mathematical conveniences for computing the positions of the planets and moons. On this approach, the large image and probably explosive points (the Bible is flawed) could possibly be averted. By its nature conceptual reasoning can elevate uncomfortable points and lift these points in strange phrases and footage which are simply understood by non-experts, in contrast to summary symbols. Galileo, the epitome of the useless and smug scientist, blindly ignored the recommendation and bought into severe bother. Kepler, not with out his faults however way more conciliatory in type than Galileo, averted an identical fiasco (he was excommunicated by the Lutheran Church — a a lot much less severe matter than a trial by the Inquisition — over an unrelated matter of non secular doctrine).
Neither is the delicate nature of conceptual evaluation an issue restricted to Galileo, Kepler, and the Renaissance. The logical and philosophical issues with quantum mechanics that puzzled Albert Einstein, Erwin Schrödinger, and Prince Louis de Broglie in the end led Einstein to infer the non-local nature of quantum mechanics, one thing that seems to have been confirmed in quite a few experiments during the last a number of many years. This quantum entanglement by which broadly separated objects preserve some type of mysterious instantaneous connection — definitely sooner than mild — raises many curious points and has been embraced by mystics, parapsychologists and others as empirical proof of the oneness of all issues claimed in most mystical programs. Quantum mechanics as an summary algorithm expressed in symbolic arithmetic raises none of those points — or, at the least, they’re nicely disguised.
Conceptual Reasoning and Evaluation
Curiously, most individuals by no means use symbolic arithmetic and symbolic manipulation. They encounter it in highschool algebra and sometimes by no means once more. For probably the most half, human beings motive with ideas, with psychological footage, and solely very hardly ever with specific numbers, mathematical symbols, symbolic formulation, or symbolic manipulation. After many years of principally failed analysis into synthetic intelligence, we now have some concept why that is. For sure lessons of geometric objects resembling circles, spheres, cubes, and so forth, there are precise symbolic formulation.
[tex] (x-a)^2 + (y-b)^2 = r^2 [/tex] (The Circle)
That is the system for a circle with arbitrary location and measurement. The radius of the circle is [tex]r[/tex]. The situation of the middle of the circle is [tex](a,b)[/tex]. We are able to do the identical with spheres:
[tex] (x-a)^2 + (y-b)^2 + (z-c)^2 = r^2 [/tex] (The Sphere)
This can be a sphere with radius [tex]r[/tex] centered at [tex](a,b,c)[/tex] in three dimensions.
Up to now, so good. What’s the symbolic system for the form of a cat? A tree? A automotive? A chair? The letter “A”? A door deal with? The problem just isn’t the symbolic system for a single occasion of a cat, a tree, and so forth. Motion pictures at the moment are stuffed with particular pc generated cats, bushes, automobiles, and so forth. However what’s the symbolic system for the category of cats, the category of bushes, the category of automobiles, and so on.? How do human beings take a look at cats — huge cats, small cats, skinny cats, fats cats, brown cats, orange cats, cats dyed purple — and acknowledge that every particular cat is an occasion of the category of cats, the idea of a cat? We do not know. Object oriented programming resembling present in Java, C#, C++ and lots of different programming languages was impressed partially by this downside, however object oriented applications nonetheless can not suppose conceptually like human beings. Varied extremely mathematical synthetic intelligence strategies resembling synthetic neural networks have been developed to resolve the identical downside, however to date they haven’t succeeded.
For many on a regular basis shapes, objects, and phenomena, we have no idea a symbolic mathematical system, in contrast to easy geometrical shapes just like the circle or sphere. One way or the other, via conceptual reasoning abilities and “instinct” human beings can motive efficiently concerning the many shapes, objects, and phenomena they encounter on daily basis with out something clearly identifiable as symbolic or numerical arithmetic. This may be very exact. Human beings have little issue choosing up and manipulating fairly advanced shapes. Computer systems and robots, even utilizing probably the most superior arithmetic that we all know, typically can not do the identical. This is the reason many frequent duties resembling clerks at comfort shops or meeting duties in factories are nonetheless carried out by human beings. This can be a very exact potential, as if the human thoughts was subconsciously computing the exact coordinates of surfaces. There may be little acutely aware consciousness of this if some type of arithmetic is in use because it most likely is.
Most main advances in energy and propulsion have concerned at the least one conceptual leap, normally a brand new structure — a brand new part or a radically new system. In lots of circumstances, these are new shapes and/or mixtures of supplies that work in a considerably totally different approach from previous programs. Since normally, the brand new shapes or constructions can’t be represented as a symbolic system, it’s troublesome to see how any recognized symbolic manipulation may discover the development. Generally, it was a psychological leap — so-called instinct. One can typically simulate a particular occasion of a brand new structure or design with trendy arithmetic and computer systems. Some important equations such because the Navier-Stokes equations stay troublesome or unattainable to simulate numerically or remedy precisely via symbolic strategies. Neglecting the issues with fixing or numerically simulating equations just like the Navier-Stokes equation, it stays the case that there isn’t a technique to categorical the overall shapes or ideas as symbolic formulation, though one can typically categorical a particular occasion as a pc or symbolic mannequin. Consequently, each symbolic manipulation and pc simulations are merely unable to discover a new form, construction, or system for energy or propulsion or many different types of mechanical invention. They are often useful in verifying an idea as soon as discovered, figuring out that it’s more likely to succeed.
In elementary physics, most main advances consisted of a conceptual leap, typically expressed in phrases or footage, adopted by the event of a mathematical system that applied the brand new idea. Kepler realized that the orbit of Mars was one thing like an ellipse. He was lucky that the ellipse was a easy geometric type that had been studied efficiently by Apollonius of Perga over a thousand years earlier than. He was principally in a position to lookup the arithmetic that matched his psychological idea. In most likely probably the most excessive instance of the separation of ideas and arithmetic, Michael Faraday constructed a psychological image of {the electrical} and magnetic fields (as pressures and circulating vortices within the hypothetical luminiferous ether) fully with out arithmetic. William Thomson (later Lord Kelvin) after which James Clerk Maxwell, Thomson’s scholar, have been in a position to translate the images into mathematical language, ultimately Maxwell’s Equations. Within the case of Faraday and Maxwell, it was not a easy matter of wanting up the arithmetic in an outdated ebook. Slightly, Maxwell needed to assemble mechanical fashions of the hypothetical ether, assign values to particular or consultant factors within the mechanical mannequin, after which infer the differential equations that comprise Maxwell’s Equations. Einstein developed the idea that gravity was on account of mass and power warping space-time nicely earlier than he was in a position, after a number of failures, to discover a particular equation that applied his idea and appeared to match sure observational measurements (notably the precession of Mercury). Schrödinger began from Louis de Broglie’s idea that the electron had a wave related to it and tried for a while to discover a wave equation that matched the spectrum of hydrogen. There are a lot of doable wave equations and Schrödinger, like Kepler earlier than him, was lucky {that a} easy, straightforward to guess system could possibly be discovered.
If one tries to carry out elementary physics purely by symbolic manipulation with none psychological visualization or conceptual evaluation, one has little or no to work with. One should principally guess symbolic formulation, typically by randomly including phrases to recognized formulation and expressions. That is very straightforward to do with the Lagrangian formalism. The literature of theoretical physics within the final forty or fifty years is crammed with guesses at Lagrangians for varied forces and phenomena and particularly the idea of the whole lot (TOE). Traditionally, physicists used ideas to slender down the quantity and vary of symbolic formulation to attempt. There was nonetheless a number of trial and error however typically the conceptual evaluation, the “instinct,” appears to have been efficient.
Conclusion
Symbolic arithmetic and symbolic manipulation are very highly effective in some circumstances. They don’t seem to be a panacea. In truth, given the present state of mathematical data, they’ve nice limitations. Most individuals have, use, and rely for his or her survival on conceptual reasoning talents on daily basis that we don’t know learn how to categorical in symbolic mathematical type or program on a pc, if that is even doable. To make main progress, even in extremely mathematical areas like pure arithmetic or theoretical physics or energy programs, we most likely must make heavy use of conceptual evaluation and visualization simply because the profitable scientists and engineers of the previous did.
Copyright © 2010 John F. McGowan, Ph.D.
In regards to the Creator
John F. McGowan, Ph.D. is a software program developer, analysis scientist, and marketing consultant. He works primarily within the space of advanced algorithms that embody superior mathematical and logical ideas, together with speech recognition and video compression applied sciences. He has in depth expertise growing software program in C, C++, Visible Primary, Mathematica, MATLAB, and lots of different programming languages. He’s most likely finest recognized for his AVI Overview, an Web FAQ (Regularly Requested Questions) on the Microsoft AVI (Audio Video Interleave) file format. He has labored as a contractor at NASA Ames Analysis Heart concerned within the analysis and improvement of picture and video processing algorithms and expertise. He has printed articles on the origin and evolution of life, the exploration of Mars (anticipating the invention of methane on Mars), and low cost entry to area. He has a Ph.D. in physics from the College of Illinois at Urbana-Champaign and a B.S. in physics from the California Institute of Know-how (Caltech). He could be reached at [email protected].
Sponsor’s message: Obtain free weekly updates about new math books. Don’t miss nice new titles within the genres you like (resembling Arithmetic, Science, Programming, and Sci-Fi): https://anynewbooks.com




![Erratum for “An inverse theorem for the Gowers U^s+1[N]-norm”](https://azmath.info/wp-content/uploads/2024/07/2211-erratum-for-an-inverse-theorem-for-the-gowers-us1n-norm-150x150.jpg)

