Think about a rope that was simply lengthy sufficient to wrap tightly across the equator of a superbly spherical earth. Now think about that the size of that rope is elevated by one meter and once more wrapped across the earth, supported in an everyday manner, in order to type an annulus. Doing issues on this manner will type a sure hole between the earth and the prolonged rope. Now think about that you just repeat the method with a golf ball. How do the 2 gaps examine?
Most individuals who perceive the issue accurately, will instantly assume that including a single meter to the rope surrounding the massive spherical earth gained’t create a lot of a spot, whereas including a single meter to the rope across the golf ball, will create a big hole. In actuality, the 2 gaps are an identical. It’s counterintuitive, however it may be confirmed simply with elementary arithmetic.
We all know that:
[tex]C = 2 pi r[/tex]
[tex]C + 1 = 2 pi R[/tex]
The place C is the size of the rope round a given spherical object, C+1 is clearly the size of the longer (by one meter) rope, r is the radius of the article (e.g. the golf ball) and R the radius of the annulus. We will categorical the 2 equations above as such:
[tex]displaystyle r = frac{C}{2pi}[/tex]
[tex]displaystyle R = frac{C+1}{2pi}[/tex]
The width of the hole between the longer rope and the article that’s considered is R-r.
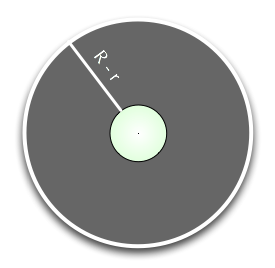
Subsequently:
[tex]displaystyle R – r = frac{C+1}{2pi} – frac{C}{2pi} = frac{1}{2pi} approx 0.159[/tex]
The hole, as you’ll be able to see, is fixed at about 16 cm, and it doesn’t rely in any manner on the scale of the radius (r) of the article at hand. That implies that the hole between the prolonged rope and the golf ball is identical as within the case of the spherical earth.
 Fairly a shocking outcome, isn’t it? This precise instance opens up the e book Inconceivable?: Shocking Options to Counterintuitive Conundrums which I obtained as a media copy within the mail. Up to now it’s been a really fulfilling and straightforward learn, chocked full of unusual paradoxes and outcomes which widespread sense would have you ever deem (virtually) not possible or counterintuitive. To make issues even nicer, the maths concerned shouldn’t be overly superior, and anybody who grasped highschool stage math, shouldn’t have any drawback following this partaking e book.
Fairly a shocking outcome, isn’t it? This precise instance opens up the e book Inconceivable?: Shocking Options to Counterintuitive Conundrums which I obtained as a media copy within the mail. Up to now it’s been a really fulfilling and straightforward learn, chocked full of unusual paradoxes and outcomes which widespread sense would have you ever deem (virtually) not possible or counterintuitive. To make issues even nicer, the maths concerned shouldn’t be overly superior, and anybody who grasped highschool stage math, shouldn’t have any drawback following this partaking e book.




![Erratum for “An inverse theorem for the Gowers U^s+1[N]-norm”](https://azmath.info/wp-content/uploads/2024/07/2211-erratum-for-an-inverse-theorem-for-the-gowers-us1n-norm-150x150.jpg)

