The Recreation of Life is an easy mobile automaton invented by mathematician John Conway. The Recreation of Life consists of a two dimensional grid of cells. Every cell might be “dwell” or “lifeless”, typically represented mathematically by 1 and 0. The grid is up to date periodically in discrete time steps in accordance with a easy rule based mostly on the cell’s neighbors, the cells instantly adjoining to the cell horizontally, vertically, and diagonally. The determine under reveals a dwell cell (black is used for a dwell cell on this article) and its lifeless neighbors. The grid is displayed for readability.

Cell Neighbors
The replace rule for the Recreation of Life is:
- A dwell cell with fewer than two dwell neighbors dies.
- A dwell cell with two or three neighbors lives on to the subsequent time step.
- A dwell cell with greater than three neighbors dies.
- A lifeless cell with precisely three dwell neighbors turns into a dwell cell within the subsequent time step.
The Recreation of Life has many attention-grabbing and entertaining properties. Amongst different options, it might implement a basic objective laptop just like the way more advanced Pentium CPU chip. There’s in depth data on the Recreation of Life on the Net. readers are referred to this on-line data in addition to the numerous conventional printed articles and books that debate the Recreation of Life. This text discusses learn how to implement the Recreation of Life in Octave, a free open-source numerical programming atmosphere that’s largely appropriate with MATLAB. Octave is accessible in each supply code and pre-compiled binaries for all three main computing platforms: MS Home windows, Macintosh, and Unix/Linux. Full supply code in Octave is offered and the outcomes of a number of simulations of the Recreation of Life are proven.
Simulations of the Recreation of Life
There are a selection of constructions within the Recreation of Life which have attention-grabbing properties. These vary from easy oscillators that cycle via a hard and fast set of patterns to advanced self-perpetuating patterns that develop and evolve indefinitely. A number of are proven under. These had been simulated utilizing an implementation of the Recreation of Life in Octave. The simulation generates a sequence of pictures exhibiting the time evolution of the Recreation of Life. These picture squences are both static GIF pictures or static JPEG pictures. The place doable, the photographs had been mixed into animated GIF sequences proven under utilizing the convert utility in ImageMagick. In some instances this proved troublesome and the photographs had been transformed to MPEG-4 video (MP4) utilizing the ffmpeg command line utility.
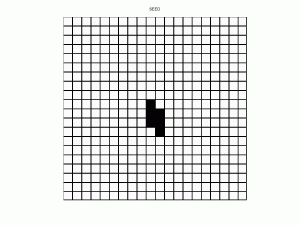
Toad Oscillator within the Recreation of Life (Click on on Picture to See Film)
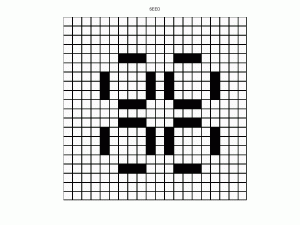
Pulsar Oscillator (Click on on Picture to See Film)
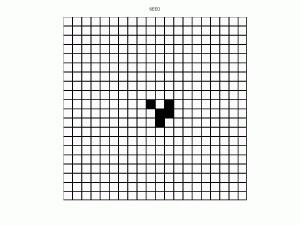
Glider in Recreation of Life (Click on under to see film)
Glider Film
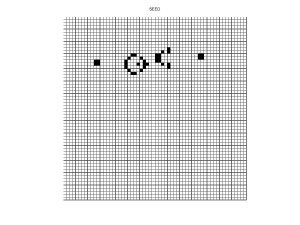
Gosper’s Gun (Generates Gliders)
Gosper’s Gun (Click on right here to see film)
Octave Code
The principle Recreation of Life simulation perform is simulate_life. This implementation makes use of a collection of nested loops to implement the replace rule in a approach that can be acquainted to customers of procedural programming languages just like the C programming language. Later, a perform simulate_life_fast is offered which implements the replace rule utilizing the “matrix” operations in Octave with no loops over the rows and columns of the Octave matrix that represents the Recreation of Life universe.
Essential Simulation
simulate_life.m
perform [] = simulate_life(myseed, niter, title, ext)
% [] = simulate_life(myseed, niter [,name, ext])
% simulate Conway's Recreation of Life
% myseed is 2nd array with values 0 or 1
% 0 is a lifeless cell
% 1 is a dwell cell
% niter is variety of iterations to simulate
% title (non-obligatory) title of simulation
% ext (optionsal) extension of picture file (default gif)
%
% Creator: John F. McGowan, Ph.D.
% E-Mail: [email protected]
%
% to make an animated gif of the sport of life
%
% Set up ImageMagick in your laptop
% command immediate>convert -delay 10 -loop 0 life*.gif sport.gif
% to make sport.gif animated gif
%
% any good net browser (resembling FireFox) can show animated GIF video
%
if (nargin < 2)
printf("ERROR: too few arguments!n");
printf("Utilization: simulate_life(myseed, number_of_iterations [,simulation_name])n");
fflush(stdout);
return;
finish
if nargin < 3
title="life";
finish
if nargin < 4
ext="gif";
finish
nx = rows(myseed);
ny = columns(myseed);
earlier = myseed;
replace = zeros(measurement(earlier));
display_array = life_grid(myseed);
imshow(!display_array);
title('SEED');
pause(1);
seed_name = sprintf("%s000.%s", title, ext);
print(seed_name);
total_live = sum(sum(earlier));
printf("%d dwell cells in seedn", total_live);
fflush(stdout);
for iter = 1:niter
% simulate one iteration/replace of sport
%
for ix = 1:nx
for iy = 1:ny
lowx = max(ix-1,1);
hix = min(ix+1, nx);
lowy = max(iy-1,1);
hiy = min(iy+1, ny);
nlive = sum(sum(earlier(lowx:hix,lowy:hiy))); % add up variety of dwell cells in neighborhood
% deal with 4 (4) nook instances
if (ix == 1 && iy == 1) || (ix == 1 && iy == ny) || (ix == nx && iy == ny) || (ix == nx && iy == 1)
n11 = earlier(cycle(ix-1,nx), cycle(iy-1,ny));
n12 = earlier(ix , cycle(iy-1, ny));
n13 = earlier(cycle(ix+1,nx), cycle(iy-1,ny));
n21 = earlier(cycle(ix-1,nx), iy);
n22 = earlier(ix, iy); % middle cell (present cell)
n23 = earlier(cycle(ix+1,nx), iy);
n31 = earlier(cycle(ix-1,nx), cycle(iy+1, ny));
n32 = earlier(ix , cycle(iy+1, ny));
n33 = earlier(cycle(ix+1, nx), cycle(iy+1, ny));
nlive = n11 + n12 + n13 + n21 + n22 + n23 + n31 + n32 + n33;
else
% non nook instances
% deal with cells at fringe of universe (deal with as closed universe)
if ix == 1
nlive = nlive + sum(earlier(nx,lowy:hiy));
finish
if ix == nx
nlive = nlive + sum(earlier(1,lowy:hiy));
finish
if iy == 1
nlive = nlive + sum(earlier(lowx:hix, ny));
finish
if iy == ny
nlive = nlive + sum(earlier(lowx:hix, 1));
finish
finish % else non nook instances
if earlier(ix,iy) == 1
nlive = nlive - 1; % do not rely middle cell
printf("dwell cell %d %d has %d dwell neighborsn", ix, iy, nlive);
fflush(stdout);
finish
if nlive < 2 % cell with fewer than 2 dwell neighbors dies
replace(ix, iy) = 0; % cell dies
elseif (nlive ==2 || nlive ==3) % cell lives on if it has 2 or 3 neighbors
if(earlier(ix,iy) == 0 && nlive == 3)
replace(ix, iy) = 1; % lifeless cell comes alive if it has precisely 3 dwell neighbors (copy)
else
replace(ix, iy) = earlier(ix,iy);
finish
elseif nlive > 3 % cell dies on account of overpopulation
replace(ix, iy) = 0;
else
replace(ix, iy) = earlier(ix,iy);
printf("error if obtained heren");
fflush(stdout);
finish
finish % loop over columns
finish % loop over rows
total_live = sum(sum(replace));
printf("%d dwell cells at iteration %dn", total_live, iter);
fflush(stdout);
earlier = replace;
filename = sprintf("%spercent03d.%s", title, iter, ext); % write picture sequence to disk
%imshow(!earlier);
display_array = life_grid(earlier);
imshow(!display_array);
title(filename);
pause(1);
print(filename);
finish % loop over iterations
finish % perform simulate_life
The perform simulate_life calls a assist perform cycle which makes use of the Octave mod perform to wrap the row and column coordinates on the edges of the Recreation of Life universe. This closes the Recreation of Life universe, giving it a torus or donut form. Within the glider simulation, the glider travels off one finish of the universe and reappears on the different finish.
cycle.m
perform [result] = cycle(n,m) % [result] = cycle(n,m) % 1 to n index wrap % end result = mod(n-1,m)+1; finish
life_grid.m
perform [display_array] = life_grid(earlier)
% [display_array] = life_grid(earlier)
%
display_array = zeros(10*measurement(earlier)); % create a bigger show array
display_array(1:10:finish,:) = 1; % create grid
display_array(:,1:10:finish) = 1;
display_array(finish,:) = 1;
display_array(:,finish) = 1;
for i = 1:rows(display_array)-1
for j = 1:columns(display_array)-1
idata = ground((i-1)/10)+1;
jdata = ground((j-1)/10)+1;
if(earlier(idata, jdata) == 1)
display_array(i,j) = 1;
finish
finish
finish
finish % finish perform life_grid
Initializing Particular Patterns
life_toad.m
perform [result] = life_toad(myseed, toad_x, toad_y) % [result] = life_toad(myseed, toad_x, toad_y) % add a "toad" oscilaltor to Conway's sport of life % myseed -- the universe array (2D) % toad_x -- x coordinate of toad % toad_y -- y coordinate of toad % % Creator: John F. McGowan, Ph.D. % Net: https://www.jmcgowan.com/ % E-Mail: [email protected] % end result = myseed; end result(toad_x, toad_y) = 1; end result(toad_x+1, toad_y) = 1; end result(toad_x+2, toad_y) = 1; end result(toad_x + 1, toad_y + 1) = 1; end result(toad_x + 2, toad_y + 1) = 1; end result(toad_x + 3, toad_y + 1) = 1; finish % perform life_toad
life_pulsar.m
perform [result] = life_pulsar(myseed, pulsar_x, pulsar_y) % [result] = life_pulsar(myseed, pulsar_x, pulsar_y) % add a "pulsar" oscilaltor to Conway's sport of life % myseed -- the universe array (2D) % pulsar_x -- x coordinate of pulsar % pulsar_y -- y coordinate of pulsar % % Creator: John F. McGowan, Ph.D. % Net: https://www.jmcgowan.com/ % E-Mail: [email protected] % pulsar = [ 0 0 1 1 1 0 0 0 1 1 1 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0; 1 0 0 0 0 1 0 1 0 0 0 0 1; 1 0 0 0 0 1 0 1 0 0 0 0 1; 1 0 0 0 0 1 0 1 0 0 0 0 1; 0 0 1 1 1 0 0 0 1 1 1 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 1 1 1 0 0 0 1 1 1 0 0; 1 0 0 0 0 1 0 1 0 0 0 0 1; 1 0 0 0 0 1 0 1 0 0 0 0 1; 1 0 0 0 0 1 0 1 0 0 0 0 1; 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 1 1 1 0 0 0 1 1 1 0 0; ]; end result = myseed; end result(pulsar_x:pulsar_x+rows(pulsar)-1, pulsar_y:pulsar_y+columns(pulsar)-1) = pulsar; finish % perform life_pulsar
life_glider.m
perform [result] = life_glider(myseed, glider_x, glider_y) % [result] = life_glider(myseed, glider_x, glider_y) % add a glider to Conway's sport of life % myseed -- the universe array (2D) % glider_x -- x coordinate of glider % glider_y -- y coordinate of glider % % Creator: John F. McGowan, Ph.D. % Net: https://www.jmcgowan.com/ % E-Mail: [email protected] % end result = myseed; end result(glider_x, glider_y) = 1; end result(glider_x+1, glider_y+1) = 1; end result(glider_x+2, glider_y+1) = 1; end result(glider_x, glider_y + 2) = 1; end result(glider_x + 1, glider_y + 2) = 1; finish % perform life_glider
life_gosper.m
perform [result] = life_gosper(myseed, gosper_x, gosper_y) % [result] = life_gosper(myseed, gosper_x, gosper_y) % add a "gosper" oscilaltor to Conway's sport of life % myseed -- the universe array (2D) % gosper_x -- x coordinate of gosper % gosper_y -- y coordinate of gosper % % Creator: John F. McGowan, Ph.D. % Net: https://www.jmcgowan.com/ % E-Mail: [email protected] % gosper = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0; 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; ]; end result = myseed; end result(gosper_x:gosper_x+rows(gosper)-1, gosper_y:gosper_y+columns(gosper)-1) = gosper; finish % perform life_gosper
High Degree Simulation Scripts
The simulations had been generated utilizing the next Octave scripts:
life.m
% John Conway's Recreation of Life in Octave % % Creator: John F. McGowan, Ph.D. % Net: https://www.jmcgowan.com/ % E-Mail: [email protected] % nx = 20; ny = 20; niter = 10; % variety of iterations of sport to simulate % 0 is a lifeless cell, 1 is a dwell cell % % blinker % myseed = repmat(0, nx, ny); % create seed for sport of life % myseed(nx/2, ny/2) = 1; % myseed((nx/2)+1, ny/2) = 1; % myseed((nx/2)+2, ny/2) = 1; % simulate_life(myseed, niter); % glider myseed = repmat(0, nx, ny); glider_x = nx/2 + 7; glider_y = ny/2 + 7; %myseed = life_glider(myseed, glider_x, glider_y); % add a toad oscillator %myseed = life_toad(myseed, nx/2, ny/2); % blinker at nook % myseed(1,ny) = 1; % myseed(nx,ny) = 1; % myseed(nx-1, ny) = 1; % add a pulsar oscillator (interval 3 iterations) myseed = life_pulsar(myseed, 5,5); simulate_life(myseed, 10, "pulsar"); % END OF FILE (Conway's Recreation of Life in Octave)
gosper_demo.m
% gosper_demo % % demo of Gosper Gun in Conway's Recreation of Life % % Creator: John F. McGowan, Ph.D. % E-Mail: [email protected] % % myseed = zeros(60, 60); myseed = life_gosper(myseed, 10, 10); simulate_life(myseed, 100, 'gosper', 'jpg');
glider_demo.m
% glider myseed = repmat(0, 20, 20); glider_x = 10; glider_y = 10; myseed = life_glider(myseed, glider_x, glider_y); simulate_life(myseed, 100, 'glider', 'jpg');
Elegant Implementation in Octave

Gosper’s Gun (Quick Implementation)
Gosper’s Gun (Click on Right here to See Film)
Octave has a lot of “matrix” or “n-dimensional array” operators and features that function on a complete Octave matrix (two-dimensional array) or n-dimensional array with out nested loops over the indices of the matrix or array. These are usually quicker, extra compact, and sometimes the coding is much less error inclined than utilizing nested loops. That is an implementation of the Recreation of Life utilizing Octave matrix operators:
simulate_life_fast.m
perform [] = simulate_life_fast(myseed, niter, title, ext)
% [] = simulate_life_fast(myseed, niter [,name ,ext])
% simulate Conway's Recreation of Life
% myseed is 2nd array with values 0 or 1
% 0 is a lifeless cell
% 1 is a dwell cell
% niter is variety of iterations to simulate
% title (non-obligatory) title of simulation
% ext (optionsal) extension of picture file (default gif)
%
% Creator: John F. McGowan, Ph.D.
% E-Mail: [email protected]
%
% to make an animated gif of the sport of life
%
% Set up ImageMagick in your laptop
% command immediate>convert -delay 10 -loop 0 life*.gif sport.gif
% to make sport.gif animated gif
%
% any good net browser (resembling FireFox) can show animated GIF video
%
if (nargin < 2)
printf("ERROR: too few arguments!n");
printf("Utilization: simulate_life(myseed, number_of_iterations [,simulation_name])n");
fflush(stdout);
return;
finish
if nargin < 3
title="life";
finish
if nargin < 4
ext="gif";
finish
nx = rows(myseed);
ny = columns(myseed);
earlier = myseed;
replace = zeros(measurement(earlier));
imshow(!myseed);
title('SEED');
pause(1);
seed_name = sprintf("%s000.%s", title, ext);
count_neighbors = [1 1 1; 1 0 1; 1 1 1];
% search for tables -- zero based mostly index
lut_live = [ 0 0 1 1 0 0 0 0 0 0 0 0]; % dwell cells with lower than 2 dwell neighbors die, 2-3 dwell, greater than 3 die (overpopulation)
lut_dead = [ 0 0 0 1 0 0 0 0 0 0 0 0]; % any lifeless cell with precisely three (3) dwell neighbors comes alive
print(seed_name);
total_live = sum(sum(earlier));
for iter = 1:niter
% simulate one iteration/replace of sport
%
nneighbors = conv2(earlier, count_neighbors, 'identical');
live_change = earlier .* lut_live(nneighbors+1); % replace the dwell cells
dead_change = !earlier .* lut_dead(nneighbors+1); % deliver lifeless cells with 3 dwell neighbors to life
replace = live_change + dead_change;
total_live = sum(sum(replace));
earlier = replace;
filename = sprintf("%spercent03d.%s", title, iter, ext); % write picture sequence to disk
imshow(!earlier);
%display_array = life_grid(earlier);
%imshow(!display_array);
title(filename);
print(filename);
finish % loop over iterations
finish % perform simulate_life_fast
Conclusion
The Recreation of Life is an easy, simple to implement, entertaining mobile automaton. It’s simple to implement the Recreation of Life in Octave (or MATLAB or SciLab). Exterior instruments resembling ImageMagick convert or ffmpeg can be utilized to simply convert the picture sequences that Octave can generate into animations in generally used codecs resembling animated GIF or MPEG-4 video. Even utilizing Octave’s matrix-oriented operators to implement the Recreation of Life, avoidign the cumbersome and customarily gradual nested loops over rows and columns, the Octave implementation remains to be gradual in comparison with a compiled C programming language implementation. This velocity challenge might be the first disadvantage to utilizing Octave, which in any other case may be very fast and handy and has a a lot decrease improvement time than low degree compiled languages resembling C.
© 2011 John F. McGowan
In regards to the Creator
John F. McGowan, Ph.D. is a software program developer, analysis scientist, and advisor. He works primarily within the space of advanced algorithms that embody superior mathematical and logical ideas, together with speech recognition and video compression applied sciences. He has in depth expertise growing software program in C, C++, Visible Fundamental, Mathematica, MATLAB, and lots of different programming languages. He’s most likely finest identified for his AVI Overview, an Web FAQ (Incessantly Requested Questions) on the Microsoft AVI (Audio Video Interleave) file format. He has labored as a contractor at NASA Ames Analysis Heart concerned within the analysis and improvement of picture and video processing algorithms and expertise. He has printed articles on the origin and evolution of life, the exploration of Mars (anticipating the invention of methane on Mars), and low cost entry to house. He has a Ph.D. in physics from the College of Illinois at Urbana-Champaign and a B.S. in physics from the California Institute of Know-how (Caltech). He might be reached at [email protected].
Admin’s message: On the lookout for some nice mathematical reads? Try our listing of must-read math books.




![Erratum for “An inverse theorem for the Gowers U^s+1[N]-norm”](https://azmath.info/wp-content/uploads/2024/07/2211-erratum-for-an-inverse-theorem-for-the-gowers-us1n-norm-150x150.jpg)

