Recognizing Patterns:
Can you find the particular pattern to each of the sequences below? See if you can guess the number that comes next for each set of numbers below!
a) 1, 1, 1, 1, 1, ?
b) 1, 2, 3, 4, 5, ?
c) 2, 4, 6, 8, 10, ?
d) 5, 10, 15, 20, ?
Easy to recognize what comes next, right? But how did you know? What pattern did each example make? That’s what we’ll be talking about in this post, sequences!
What is a Sequence?
Let’s start with a formal definition. A sequence is a list of numbers or objects that are in a particular order and form a pattern. Each example above is a different type of sequence that follows a specific pattern! That’s why we were able to easily find the successive term of each sequence (solution to each example below).
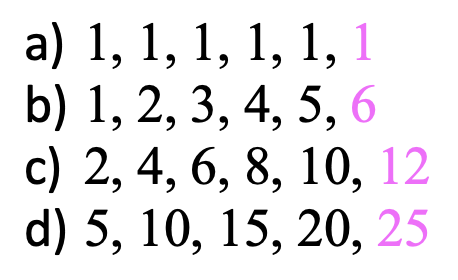
The above examples of sequences are just a snippet of what a sequence can look like, but there are so many sequences that exist! There is even a website that compiles every sequence in the world possible, called The On-Line Encyclopedia of Integer Sequences (OEIS), it’s like a kind of dictionary but for sequences! They also accept new sequences to their website. After reading this post, see if you can come up with your own sequence to add to their encyclopedia!
Types of Sequences:
There are so many different types of sequences! Sequences can take so many different forms, they can be infinite sequence where they can go on forever, or they can be finite sequence where they have an end. A sequence can be based on addition, subtraction, multiplication, division, or even based on the value of the previous term! Let’s take a look at each type of sequence one step at a time with an example for each:
Types of Sequences
Arithmetic Sequence
Geometric Sequence
Recursive Sequence
Finite Sequences
Finite Arithmetic Series
Finite Geometric Series
Infinite Sequences
Infinite Geometric Series
Special Sequences
Fibonacci Sequence
Summing Every number from 1 to 100
Arithmetic Sequence:
Arithmetic sequences are a sequence of numbers that form a pattern when the same number is either added or subtracted to each successive term. Take a look at the example of the of the arithmetic sequence below. Notice we are adding 2 to each term in the sequence 4, 6, 8, 10, … below. The number we add to each term in this sequence (in this case 2), is called the common difference. If we were to find the next term in the example of the sequence below, the next term of the sequence would be 12 (10+2=12).
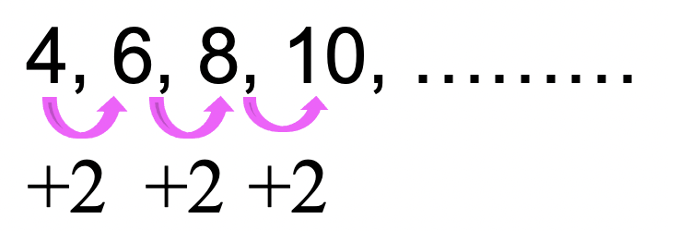
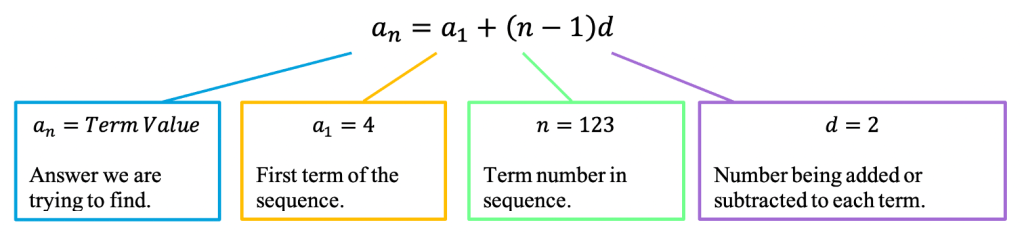
Sometimes, we are asked to find not just the next term, but a term further down the line in the sequence. For example, what if we were asked to find the value of the 123rd term? That’s where the arithmetic sequence formula would come in! Check out the explicit formula below:
an=a1+(n-1)d
a1=First Term
n=Term Number in Sequence
d=Common Difference (Number Added/Subtracted to each Term in Sequence)
Now, to find the 123rd term of the above sequence, we would plug in the following values into our formula to solve. Notice the common difference here is still 2, because it is the number we are adding to all the terms in our sequence.

Notice the above arithmetic sequence is a an example of an infinite sequence! This means that we can continue finding terms for this sequence forever!
Want another example? For more examples and a step-by-step video on arithmetic sequences, check out the resources here and below:
Geometric Sequence:
Geometric sequences are a sequence of numbers that form a pattern when the same number is either multiplied or divided to each subsequent term. Take a look at the example of a geometric sequence 4, 8, 16, 32, … below. Notice we are multiplying 2 to each term in the sequence below. The number that is multiplied to each term in the sequence is called the common ratio, which in the case of the geometric sequence below is 2. If the pattern were to continue, the next term of the sequence above would be 64, since 32 x 2=64.
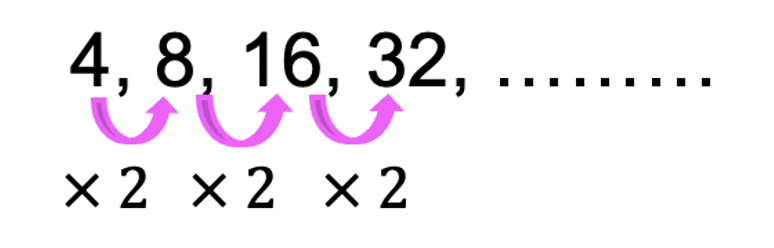
Sometimes, we are asked to find not just the next term, but a term far down the line in the sequence, for example, what if we were asked to find the value of the 15th term? That’s where the geometric sequence formula would come in!
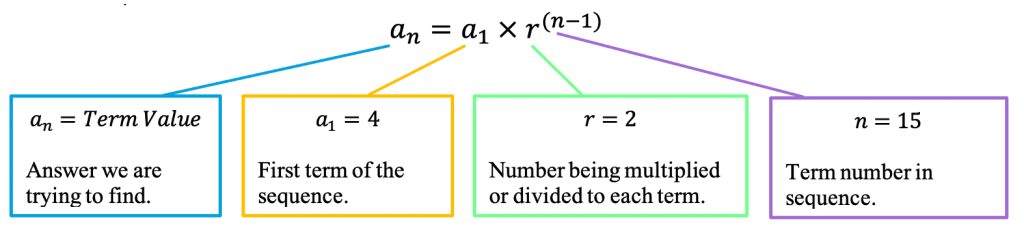
an=a1r(n-1)
a1 = First Term
r=Common Ratio (Number Multiplied/Divided to each Term in Sequence)
n= Term Number in Sequence
To find the 15th term of the above sequence, we would need to plug in the following values into our formula to solve:

Notice the above geometric sequence is a type of infinite sequence! This means that we can continue finding terms for this sequence, forever!
Want another example? For more examples and a step-by-step video on geometric sequences, check out the resources here and below:
Recursive Sequences:
A Recursive Formula is a type of formula that forms a sequence based on the previous term value. These can be based on arithmetic sequences or a geometric sequences, the sequence type does not really matter, as long as each successive term is based on the previous term. What does that mean? Check out the example below for a clearer picture:
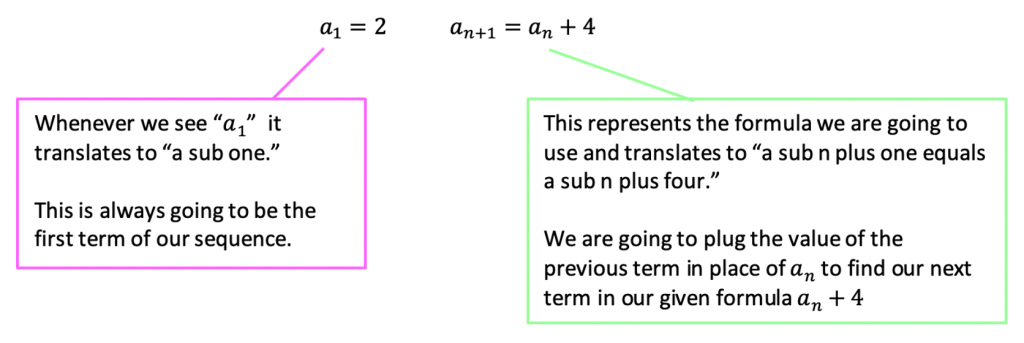
What are the first 5 terms of a recursive sequence given the following recursive formula:
First, let’s decode what this says:
Now, let’s see our formula in action! Notice below, we start with the first term, a1=2. Then we use 2 to plug into our formula for the second term to get 2+4=6, and we continue the pattern all the way through for the first five terms, to get our answer.

Recursive Sequence: Now that have used our recursive formula, notice it gave us this nice, beautiful sequence represented by each term circled in pink above, 2, 6, 10, 14, 18. That is our recursive sequence, and the answer to our question! Notice in this example, we have an infinite sequence that we can keep finding terms for, but since our question asked for the first 5 terms, we stopped here.
Want another example? For more examples and a step-by-step video on recursive sequences, check out the resources here and below:
Finite Sequence and Series:
Now that we have gone over infinite sequences (Arithmetic, Geometric, Recursive), let’s dive into finite sequence and series!
What’s the difference between a sequence and a series? We know what sequences are, but what is this new word “series” all about? Well, what if we had the first 5 terms of a sequence, but now, we want to add them all together? That is a series, more specifically a finite series since we only want to add the first five terms! Another term you might see that describes a finite sequence is “Partial Sum” or “Partial Sums” because we are summing only part of the sequence.
Finite Arithmetic Series:
A finite arithmetic series happens when we take the terms of an arithmetic sequence and we sum a finite number of them together. Basically, we know that the arithmetic sequence gives us the following terms:
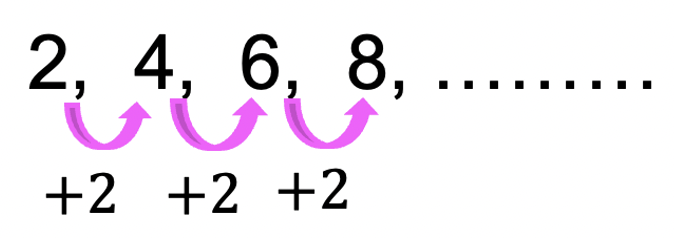
But now we want to sum all these terms together:
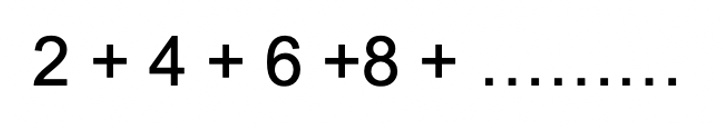
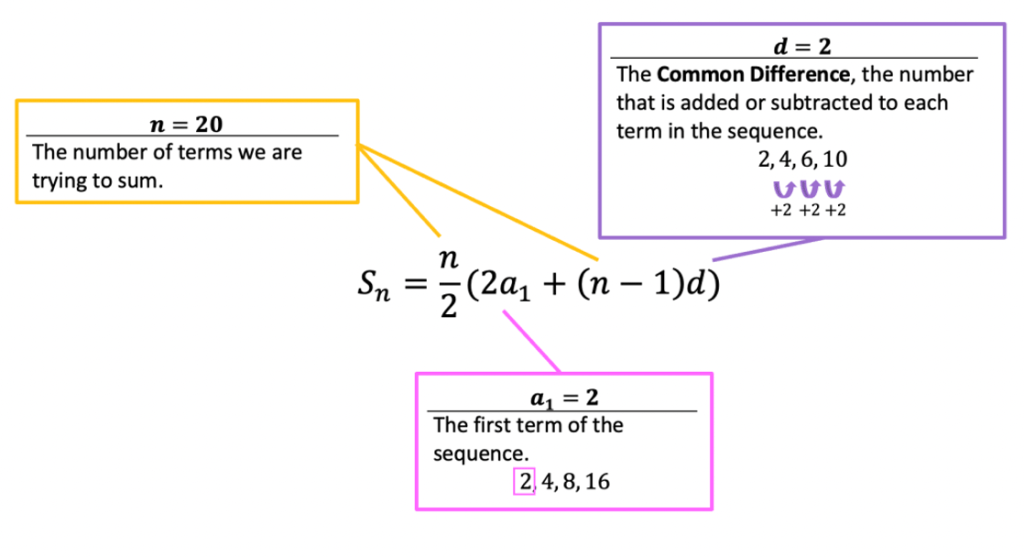
How would we be able to find the partial sum of the first 20 terms of an arithmetic sequence? Well, we could sit there and crunch our numbers one by one on a calculator, or we could plug them into the arithmetic finite sequence formula below:
Sn=(n/2)(2a1+(n-1)d)
n=Number of Terms we want to Sum
d=Common Difference
a1=First Term
To find the sum of the first 20 terms of the above sequence, we would need to plug in the following values into our formula to solve. Notice that in this case, the common difference is 2, since each subsequent term is being added by 2.

For more examples and a step-by-step video on how to find the finite length of a Finite Arithmetic Series, check out the resources here and below:
Finite Geometric Series:
A finite geometric series happens when we take the terms of a geometric sequence, and we sum them together. Basically, we know that the geometric series gives us the following terms:
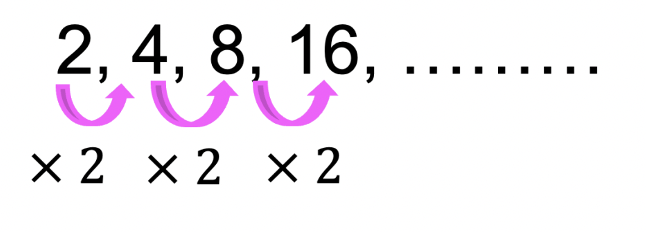
But now we want to sum all these terms together:
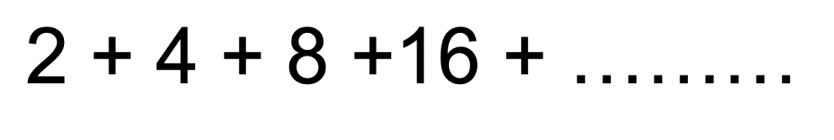
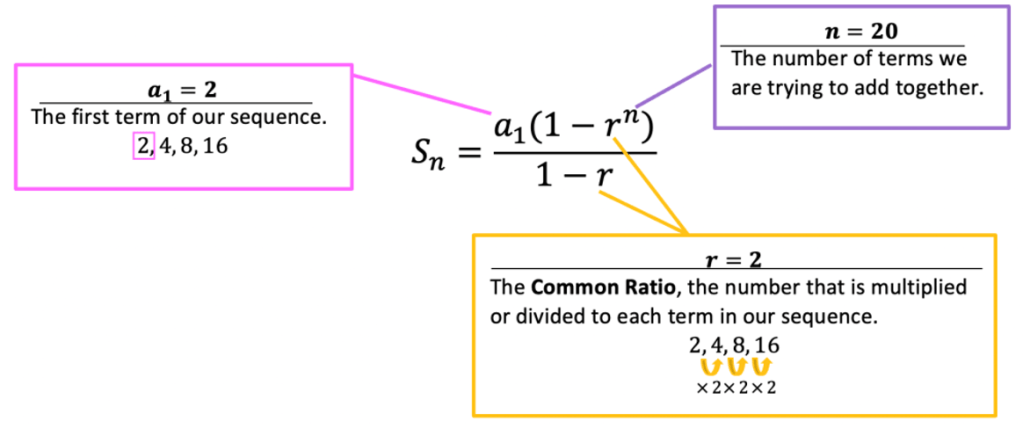
How would we be able to find the partial sums of the first 20 terms of a geometric sequence? Well, we could sit there and crunch our numbers one by one on a calculator, or we could plug them into the formula below:
Sn=a1 (1-rn)/(1-r)
a1=First Term
n=Number of Terms we are Summing together
r=Common Ratio

For more examples and a step-by-step video on finite sequences and Geometric Series, check out the resources here and below:
Infinite Sequences:
An infinite sequence is one in which the sequence just keeps going and going infinitely with no end. We have already seen examples of this earlier in this post when looking at an arithmetic sequence or geometric sequence. But now, we want to ask ourselves, what would happen if we were to add an entire infinite sequence, by adding together each term within the sequence?
When it comes to adding an infinite arithmetic sequence together, the arithmetic sequence always diverges to infinity. On the other hand, an infinite sequence that is also a geometric sequence, can either diverge to infinity, or converge to a number. If the idea of converging or diverging to infinity, doesn’t make sense yet, that’s ok, keep reading and we’ll go over everything!
Infinite Geometric Series:
An infinite geometric series happens when we take the terms of a geometric sequence, and we sum them together, all of them together, starting with the first term, going all the way to infinity. Basically, we know that the geometric series gives us the following terms:
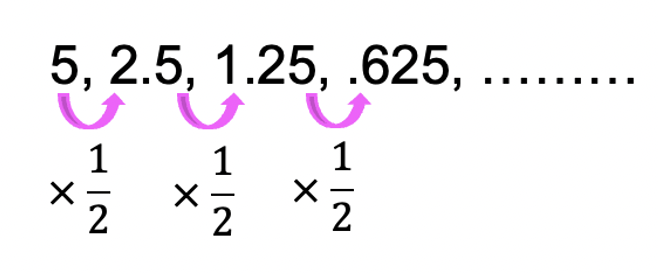
But now we want to sum all these terms together, from the first term all the way to infinity.
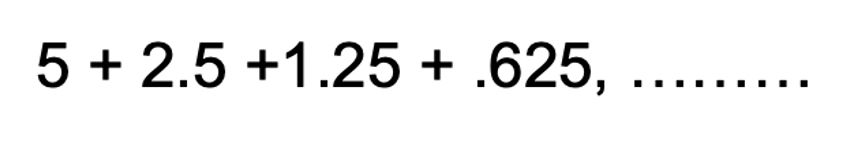
But wait, how do we know if it is even possible to sum together a geometric sequence starting with the first term and adding until infinity? Well, it all depends on divergence vs. convergence. If the common ratio is between -1 and 1, that means that the sum to infinity will converge and we can find the value of the sum of an infinite geometric sequence. If the common ratio has any other value otherwise it will diverge to infinity.
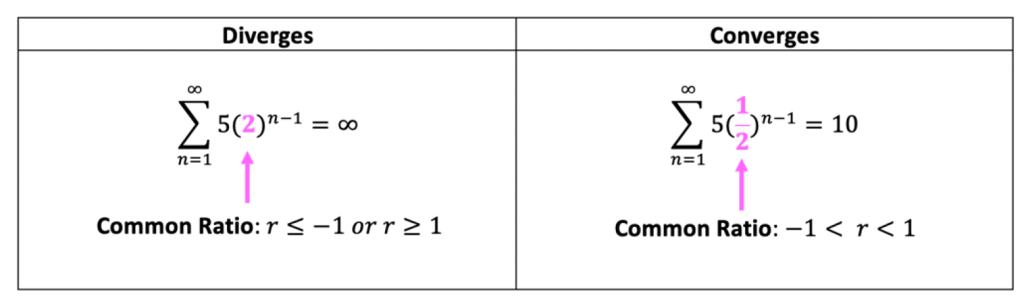
*Also here is a reminder of what a geometric sequence looks like, for anyone who needs it!
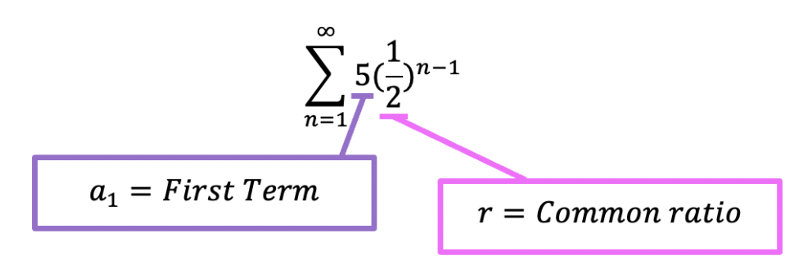
Now, let’s see if the following geometric series converges or diverges:

Since, we know it converges based on the common ratio, we know we can find the value of the infinite sum! Let’s use the formula below:
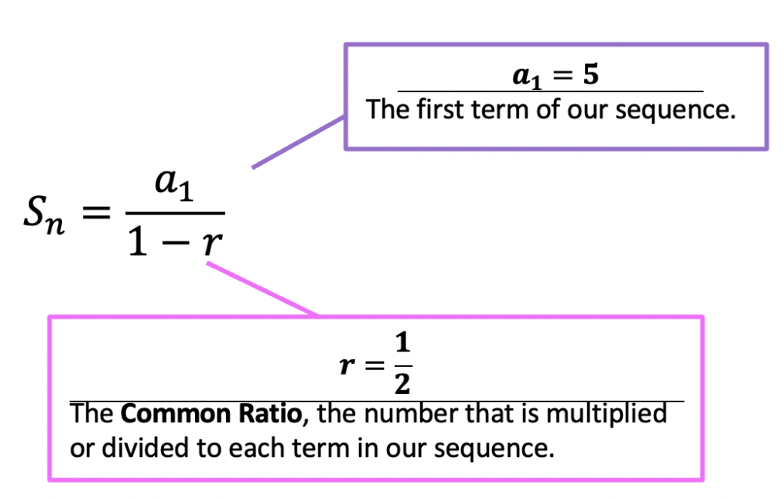
Sn=a1/(1-r)
a1=First Term
r=Common ratio
Next, let’s plug in our value into the formula:
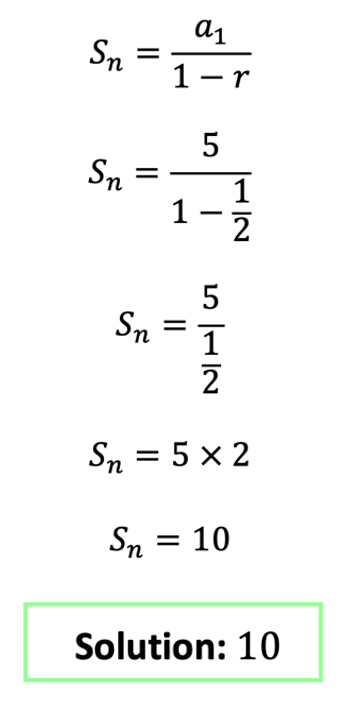
For more examples and a step-by-step video on Infinite Geometric Series, check out the resources here and below:
Special Sequences
Fibonacci Sequence – The Most Famous Sequence!
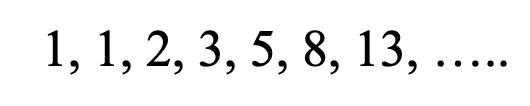
The above sequence, known as the “Fibonacci Sequence,” is the most famous sequence in the world! How can a sequence be so famous? Why is it so special? Well, we’ll get to that in a minute, but before we do, can you see how the Fibonacci Sequence forms a pattern? What would be the next term?
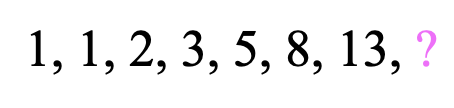
Take your time, trying to figure out the next term of the sequence before taking a peak at the answer below:
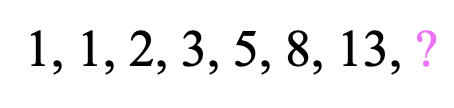
Why!? Solution Explained
The next term of the Fibonacci sequence is 21! The pattern of this famous sequence is all about adding the two previous terms together. That’s how we get 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, which brings us to get our missing term, 8+13=21. Take a look at how this sequence works below:
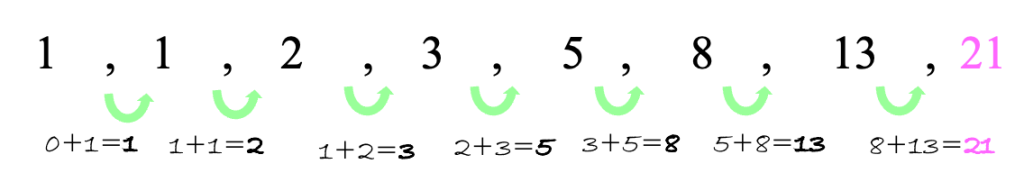
Why is the Fibonacci Sequence Famous?
Now that we know the secret pattern behind this sequence, let’s look at why the Fibonacci sequence is so special! The Fibonacci sequence’s main claim to fame is that it is found throughout art, architecture and even in nature via the golden ratio.
The Golden Ratio is a proportion that is considered to be the most pleasing ratio to the human eye! You may also know the Golden Ratio as the golden mean, the divine proportion, phi, or the Greek letter ϕ. It is an infinite and irrational number that approximates to 1.618 and is found by adding two numbers together and then dividing by the larger number and if these same two numbers are then set equal to the larger number divided by the smaller number successfully, then the two numbers are a golden ratio equal to 1.618! If this sounds too confusing to imagine, just take a look at the formula below:
Is it a Golden Ratio?
If the following formula holds true, then yes!
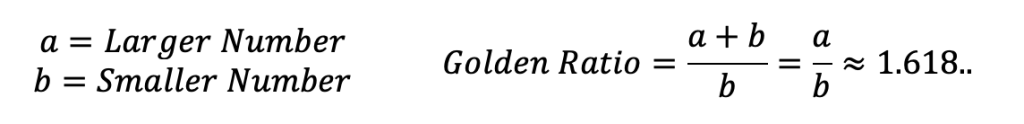
What is amazing about this ratio, is that it can be related back to the Fibonacci Sequence!
The Golden Ration + Fibonacci Sequence:
If we were to take the sequential numbers found within the Fibonacci sequence (1,1,2,3,5..), and plug them into the golden ratio formula above, it would approximate to the golden ratio value, 1.618, the further along in the sequence we go.
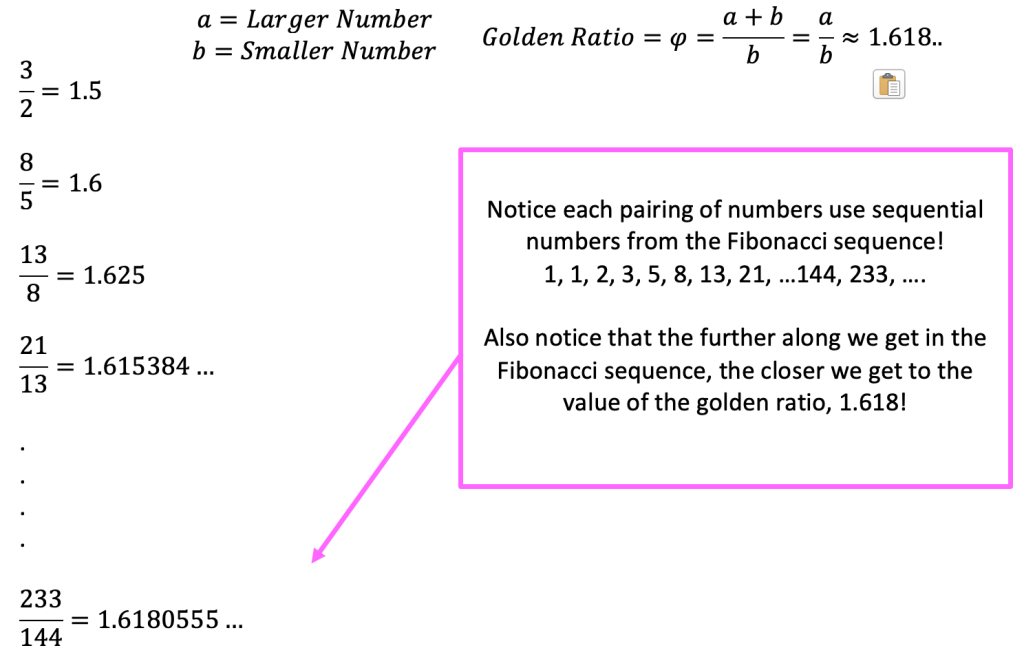
The Golden Ratio + Art + Architecture + Nature:
If we were to draw a rectangle that has golden ratio proportions, we would get the golden rectangle below.

Let’s draw a golden rectangle, within our golden rectangle to see what happens:
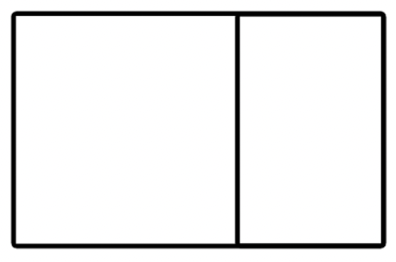
What happens if we continue this specific pattern and keep drawing in golden rectangles within itself?
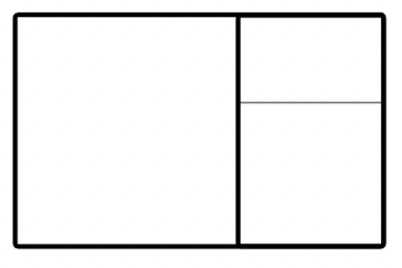
Until eventually we get something like this….
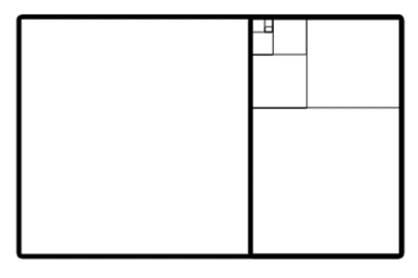
The proportion between the width and height of these rectangles is 1.618 and can also be shown as the proportion between any two numbers in the Fibonacci sequence as the sequence approaches infinity.
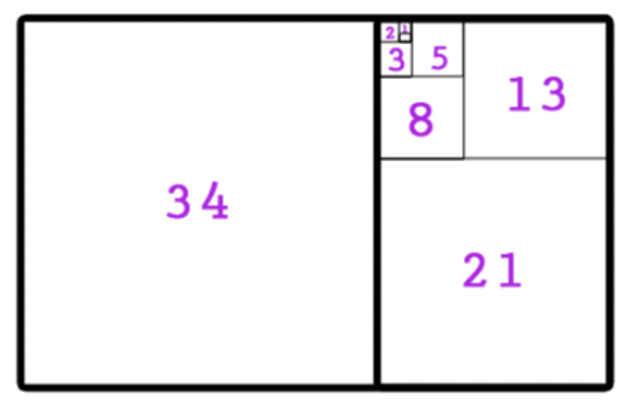
The above pattern, when all lines are connected form a spiral that can be found within art, architecture, and nature itself! Below we have a picture of the Parthenon, the Mona Lisa, a shell, and the Taj Mahal.

The Golden Ratio + YOU:
Want to know if you yourself has a face that fits the golden ratio?! Try measuring your face horizontally and vertically and plug in those values into the golden ratio formula, dividing the larger number by the smaller number. What did you get? Something close to 1.6 maybe!?
The Golden Ratio + Resources:
If you’re looking to learn more about the Golden Ratio, be sure to check out these resources here.
Donald Duck’s – Mathmagic Land:
Video shows how the golden ratio works and where we can find it! https://www.youtube.com/watch?v=U_ZHsk0-eF0&t=1s
Investopedia + Golden Ratio:
Learn how the Fibonacci Sequence connects to the modern-day stock market! https://www.investopedia.com/articles/technical/04/033104.asp
The Golden Ratio + Mathematics:
Learn where you will see the Golden Ratio in mathematic equations and shapes!
https://www.mathsisfun.com/numbers/golden-ratio.html
Summing Numbers from 1 to 100:
Now that we’ve discussed the most famous sequence, let’s talk about the most well-known sequence, which are just plain old-fashioned natural numbers, starting at 1 and counting to infinity! The sequence we all grew up with and learned to love, yes, natural numbers:
1,2,3,4,5, ….100, …..
What if we were tasked with summing all the numbers from 1 to 100? How would we do that? Well, believe or not, there is a formula to adding all of these numbers together, that was discovered by a famous mathematician named Johann Karl Friedrich Gauss. Apparently, he came up with this pattern after being assigned to add all the numbers from 1 to 100 as an elementary school student! The teacher thinking this would be perfect “busy” work for her class did not see it coming!
How to Sum 1 to 100:
Gauss found a pattern, when adding together the numbers 1 to 100. He looked at the big picture, recognizing that the sum between pairs of numbers from the beginning of the sequence and at the end of the sequence were the same throughout the entire list of numbers! For example, 1+100=101, 2+99=101, 3+98=101, and this pattern continues between all the numbers from 1 to 100! Take a look:
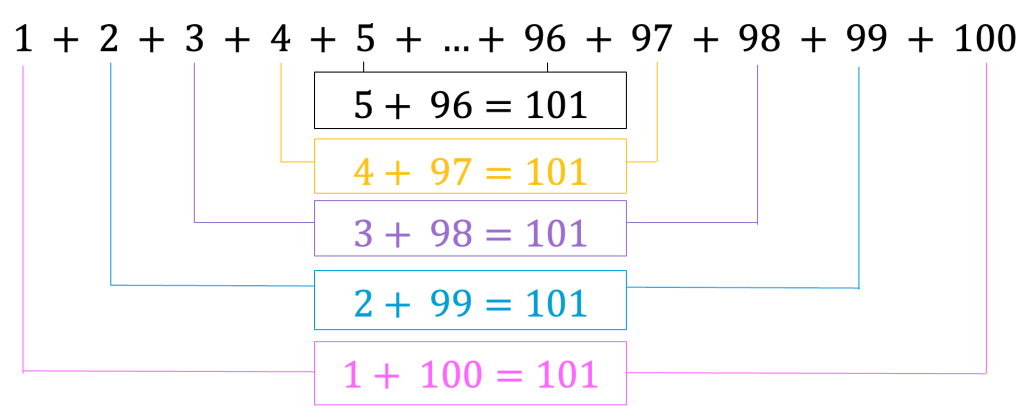
Formula and Solution:
Noticing this pattern, lead Gauss to come up with the following formula to sum every number from 1 to 100:
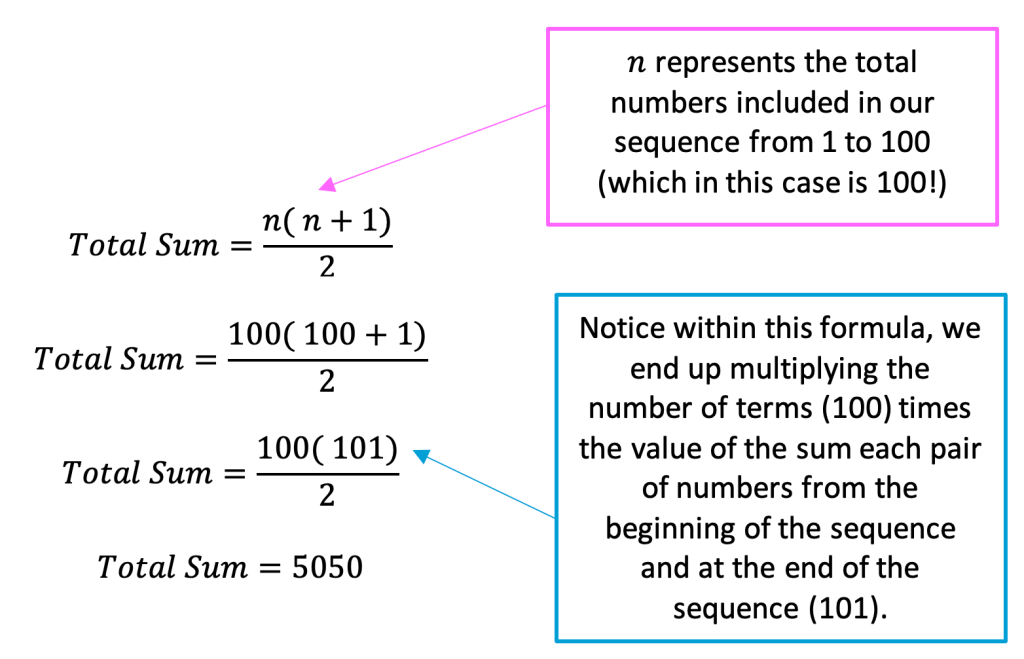
Above we use the formula to sum every number from 1 to 100 but it can be used to find other sums as well! If you’re wondering where in the world the above formula even came from, try testing it out with a smaller sum, summing numbers from 1 to 10 and see what happens!
Just like we find the sum in an arithmetic or geometric series, we can find the sum of other types of sequences, as we see here with natural numbers! We can even realize that summing numbers 1 to 100 is like summing an arithmetic sequence with a common difference of 1. Hidden patterns and formulas are used to solve all different types of sequences we haven’t even gone over in this post. But let this post guide you with the basics! See if you can find the pattern of any sequences that you find (in this post, in class, or in the street walking around, as sequences are found there too).
If you’re looking for more resources, check out this website that connects Gauss’s Summation formula to arithmetic sequences found in the real world here.
I hope you find this overview of sequences helpful! If there is anything you’d like me to go over more or if you have any questions, please let me know in the comments. Also, please check us out on social media for the latest MathSux videos, lessons, practice, questions, cheat sheets, and more! Happy calculating!
Facebook ~ Twitter ~ TikTok ~ Youtube
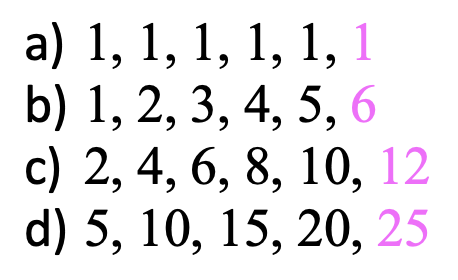




![Erratum for “An inverse theorem for the Gowers U^s+1[N]-norm”](https://azmath.info/wp-content/uploads/2024/07/2211-erratum-for-an-inverse-theorem-for-the-gowers-us1n-norm-150x150.jpg)

